(10)

Ponieważ odcinków było pięć. średnia wartości prędkości jest równa 3. Dyskusjo niepewności pomiarowej

Niepewność pomiarową policzymy jako średnią niepewność kwadratową.

—

■Hf

Av = 1-^-./)=5.

Wynik pomiarów zapisujemy w postaci

v = v ± Av.

II. Ruch prostoliniowy jednostajnie zmienny

1. Wiadomości wstępne

Rozważmy ciało poruszające się po linii prostej, które w chwili t« ma prędkość ^ a w chwili t > to prędkość % > . Jak z tego wynika w czasie:

A/=r-r₀,

prędkość ciała zwiększa się o

Av = v-i>₀.

Wprowadzamy wielkość fizyczną zwaną przyspieszeniem:

Przyspieszeniem średnim j| nazywamy wielkość fizyczną równą stosunkowi przyrostu prędkości óv do czasu, w którym ten przyrost nastąpił.

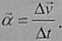
Przyspieszenie jest wektorem. Wymiar przyspieszenia:

Rozważmy przypadek ruchu prostoliniowego, w którym:

® = constans.

W ruchu takim wartość przyspieszenia średniego Jest rtmi wartości przyspieszenia chwilowego.

Jeżeli w rozważanym ruchu zwrot przyspieszenia jest zgodny ze zwrotem wektora prędkości, to ruch Inki nazywamy ruchem jednostajnie przyspieszonym. Zgodnie z definicją przyspieszenia

fi

AP v - v₀ Al | t-t, ¹

przyjmując to = 0 otrzymujemy:

stąd

v = P₀+ar.

Ponieważ ruch taki odbywa się po prostej będącej kierunkiem “. a zwrot wektorów możemy zaznaczyć podając „+" lub nie musimy korzystać z zapisu wektorowego i tym samym możemy napisać;

^v = ^vo + of.

Stojący przed przyspieszeniem znak „+” wskazuje, że ruch jest ruchem jednostajnie przyspieszony. Szczególnie przypadkiem ruchu jednostajnie przyspieszonego jest ruch bez prędkości początkowej (^vo = Ó), wtedy

■ _ry = al.

21