0044

45

§ 2. Twierdzenia o granicach ułatwiające znajdowanie granic

Z twierdzenia tego wynika dopuszczalność przejścią do granicy w nierówności (słabej); z x>,>yn można wnioskować, że limx„>lim y_n.

Znak > może być oczywiście wszędzie zastąpiony znakiem <.

Zwracamy uwagę czytelnika na to, że z nierówności ostrej x_n>y„ na ogół nie wynika ostra nierówność dla granic limx„>limy_n, a tylko, jak dawniej, nierówność słaba: lim x„^limy„. Tak na przykład 1 jn> — \jn przy wszystkich n, a tym niemniej

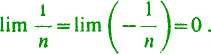
Przy ustalaniu istnienia i wielkości granicy ciągu bywa niekiedy użyteczne twierdzenie: 3° Jeżeli ciągi {*„}, {>’„}, {z„} spełniają zawsze nierówności

x«.

przy czym ciągi {.*:„} i {z„} mają wspólną granicę a:

lim x„ = lim ż„ = a ,

to i ciąg {>’„} ma tę samą granicę

lim J’„ = a .

Niech dane będzie dowolne e>0. Dla tego e można przede wszystkim znaleźć taki wskaźnik N', te przy n>N'

a — s<x_n<a + £.

Dalej znajdziemy taki wskaźnik A"', że przy n>N" jest

a— £<z„<a + e .

Niech A będzie większe niż obydwa wskaźniki N' i N"; wówczas przy «> N spełnione są obie poprzednie nierówności podwójne, a więc

a-e<x_B<y„<z_n<a + e.

Otrzymaliśmy więc w końcu, że przy n > N jest

a— £<y_n<a + £,    czyli |y_B —u|<£.

Tak więc rzeczywiście \\my„ = a.

Z twierdzenia tego wynika w szczególności następujący wniosek: jeżeli przy wszystkich n

a^yn^n

i wiadomo, że z_n->a, to również y„-*a. Zresztą wniosek ten łatwo również dowieść bezpośrednio.

Twierdzenia 1°, 2° i 3° łatwo przenieść również na przypadek granic nieskończonych.