0150

151

§ 5. Własności funkcji ciągłych

86. Pojęcie ciągłości jednostajnej. Jeżeli funkcja f(x) jest określona w pewnym przedziale SC (domkniętym lub nie, skończonym lub nie) i ciągła w punkcie x₀ tego przedziału, to

lim/(x)=/(x₀)

X-*XO

lub (w języku epsilonów i delt, 66): dla każdego e>0 istnieje takie S>0, że

|x-x₀|<<5 pociąga za sobą |/(x)-/(x₀)|<s•

Załóżmy teraz, że funkcja /(x) jest ciągła w całym przedziale SC, czyli jest ciągła w każdym punkcie x₀ tego przedziału. Wówczas dla każdego punktu x₀ z SC z osobna dla danego e istnieje <5, które odpowiada mu we wspomnianym powyżej sensie. Przy zmianie x₀ w prze

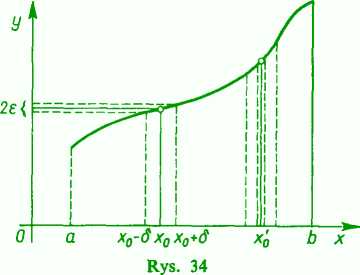
dziale SC, nawet przy nie zmienionym e, liczba <5 będzie się na ogół zmieniać. Jeden rzut oka na rysunek 34 wystarcza, żeby przekonać się, że liczba 3 dobra dla części przedziału, gdzie funkcja zmienia się wolno (wykres ma spadek łagodny), może okazać się o wiele za duża dla części przedziału, gdzie funkcja zmienia się szybko (wykres ma spadek bystry). Innymi słowy: liczba Ó zależy na ogół od e i od x₀.

Gdyby chodziło o skończoną ilość wartości x₀ (przy niezmiennym e), to dla skończonej ilości odpowiadających im liczb 3 można byłoby wybrać liczbę najmniejszą, która byłaby oczywiście dobra równocześnie dla wszystkich rozważanych punktów x₀.

Jeżeli jednak mamy do czynienia z nieskończonym zbiorem wartości x₀ zawartych w przedziale SC, to tak rozumować już nie można: wartościom tym (przy stałym e) odpowiada nieskończony zbiór liczb 6, wśród których można, być może, znaleźć również liczby dowolnie małe. Tak więc dla funkcji /(x) ciągłej w przedziale SC powstaje pytanie: czy istnieje przy danym e>0 takie <5>0, które byłoby odpowiednie dla wszystkich punktów x₀ z tego przedziału?

Jeżeli dla dowolnej liczby e>0 istnieje taka liczba <5>0, że

|x - x₀1 < 5    pociąga za sobą    | /(x) -/(x₀) | < e,

dla dowolnych punktów x„ i x z przedziału SC, to funkcję/(x) nazywamy jednostajnie ciągłą w przedziale SC.