0193

194

III. Pochodne i różniczki

Dowód. Niech na przykład f(x) osiąga w punkcie c wartość największą. Przypuszczenie, że f'(c) 0 prowadzi do sprzeczności: albo f\ć)>0 i wtedy, jeśli x>c jest dostatecznie bliskie c, to/(x)>/ (c) na podstawie lematu, albo /'(c)<0 i wtedy, jeśli x<c jest dostatecznie bliskie c, to f{x)>f (c). W obu wypadkach/(c) nie może być największą wartością funkcji f(x) w przedziale 9C. Otrzymana sprzeczność daje dowód twierdzenia.

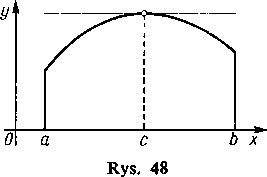
Przypomnijmy sobie [91, 92] interpretację geometryczną pochodnej y'=f'(x) jako współczynnika kątowego stycznej do krzywej y=f{x). Znikanie pochodnej/'(c) oznacza geometrycznie to, że w odpowiednim punkcie tej krzywej styczna jest równoległa do osi x, poglądowo ilustruje to rys. 48.

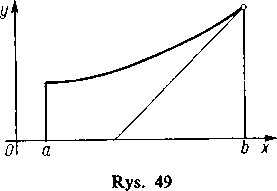
W dowodzie wykorzystaliśmy w sposób istotny założenie, że c jest punktem wewnętrznym przedziału, ponieważ rozpatrywaliśmy zarówno punkty x leżące na prawo od c jak i punkty x leżące na lewo od c. Bez tego założenia twierdzenie przestałoby być słuszne. Jeśli funkcja f(x) określona w przedziale domkniętym osiąga swoją wartość największą (najmniejszą) na jednym z końców tego przedziału, to pochodna /'(*), jeśli w tym końcu istnieje, może nie być zerem. Proponujemy czytelnikowi znaleźć odpowiedni przykład. Geometrycznie fakt ten zilustrowany jest na rysunku 49.

Jako zastosowanie twierdzenia Fermata udowodnimy pewne ciekawe twierdzenie

0    pochodnej funkcji ciągłej.

110. Twierdzenie Darboux. Udowodnimy

Twierdzenie (Darboux). Jeśli funkcja f{x) ma pochodną skończoną w przedziale (a, bj (^ł), to funkcja f'(x) przybiera co najmniej raz każdą wartość pośrednią między f\a)

1    f\b).

Dowód. Załóżmy najpierw, że f'(d) i f'(b) mają różne znaki, na przykład f'(a)>0, a f'(b)< 0; udowodnimy istnienie między punktami a i b takiego punktu c, w którym pochodna znika. Rzeczywiście, z istnienia pochodnej skończonej f\x) wynika ciągłość funkcji /(x) [96°, 2], a wtedy na podstawie drugiego twierdzenia Weierstrassa [85] /(x) osiąga w pewnym punkcie c swą wartość największą. Ten punkt c nie może pokrywać się ani z punktem a, ani z punktem b, ponieważ zgodnie z lematem / (jc) jest większe od

O Zakładamy przy tym, że w punkcie a istnieje pochodna prawostronna, a w punkcie b — pochodna lewostronna. W dalszym ciągu będziemy oznaczali je po prostu /'(u) i f'(b).