0207

208

III. Pochodne i różniczki

6) Wielomiany Legendre'a. Na zakończenie zatrzymamy się na ważnych wielomianach noszących nazwę wielomianów Legendre'a. Są one określone równością

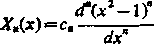
gdzie współczynnikom c, nadajemy takie lub inne wartości w zależności od tego, jak jest wygodniej.

Przede wszystkim przekonamy się, że wielomian X„(x) stopnia n ma n różnych pierwiastków rzeczywistych i że wszystkie te pierwiastki są zawarte między —lal. Dla uproszczenia założymy na razie, że e„=l.

Łatwo zauważyć, że funkcja (x*—l)"=(x—lyO^-f-l)* i jej kolejnych n—1 pochodnych są równe zeru dla x— ± 1. Wówczas jej pierwsza pochodna będzie miała na mocy twierdzenia Rolle’a [111] pierwiastek między —1 a +1. Na mocy tego samego twierdzenia druga pochodna będzie miała dwa pierwiastki między —1 a +1 itd. aż do pochodnej rzędu n—1 włącznie, która oprócz pierwiastków —1 i +1 będzie miała jeszcze n—1 pierwiastków między —1 a +1. Stosując do niej jeszcze raz twierdzenie Rolle’a dojdziemy do tego, co chcieliśmy udowodnić.

Zachowując współczynniki c„ = 1, znajdziemy teraz wartości wielomianu X„(x) dla x=+l i x = — 1.

Rozpatrując potęgę (X¹ — !)" jako iloczyn (x+l)"(x—1)", możemy napisać na podstawie wzoru Leibniza

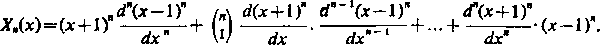
Wszystkie składniki poczynając od drugiego zawierają czynnik x—1, są więc równe zeru dla x= 1 i jest oczywiście A^r„(l)=2"-n!.

Analogicznie otrzymujemy X,(—1)=(— l)"-2"n!.

Jeśli we wzorze, dającym ogólną definicję wielomianu Legendre’a X„(x), przyjmiemy w szczególności

1

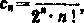
to otrzymamy wielomian najczęściej spotykany. Będziemy go dalej oznaczali przez /’„(*). Charakteryzuje go to, że w punktach x=l i x= —1 przybiera odpowiednio wartości

JWD-l, Pn(-!)=(-!)".

Za pomocą wzoru Leibniza możemy łatwo stwierdzić, że wielomiany Legendre’a X,(x) spełniają następujący związek:

(x² -1) X" +2xXi-n(.n+l)X_n=0,

który odgrywa ważną rolę w teorii tych wielomianów.

Rzeczywiście, niech y—(x² —1)*, wtedy

y'=2nx(.x² — l)"^-1, tak że (x^x—l)y'=2nxy.

Obliczmy teraz pochodne rzędu n-fl obu stron ostatniej równości; według wzoru Leibniza

(x²-1) y⁽"⁺²⁾+(n + l)2xy^{"⁺ⁱ⁾    ■ 2y™=2nxyⁱ"⁺¹⁾+(n+l)2ny^<’\

Stąd

(x²-l)y^+2>

(x²-l)y⁽’^+2>+2xy^l" ^{+ 1)}-n(n + l)y™=0,

po pomnożeniu przez c„=l/2"n! otrzymujemy zależność, którą chcieliśmy udowodnić.