052

52

2. Zmienne losowe

Dowód Ponieważ Pr(X > jc) = 1 — <E>(jc) — <ł>(— x), to

Pr(|X — m| > 3<t) = Pr ^

X — m

a

>3 =2(1-<D(3))

= 2-0.00135 = 0.0027 <0.01.

□

Z faktu 2.4,1 wynika, że

Pr(X 6 (m — 3<J,/n-f 3<r)) > 0.99.

Dla rozkładów innych niż normalny nierówność (2.4.10) nie musi być prawdziwa. Widać to z następującego przykładu.

Przykład. Dla zmiennej losowej X o gęstości

/w =    >

gdzie X > 0 jest EX = 0, gdyż f(x) jest funkcją parzystą, a całka

co    oo

xf(x) clx — 2 I xf(x)dx

o

jest bezwzględnie zbieżna i równa 1 jX (będąc wartością oczekiwaną w roz- • kładzie wykładniczym). Wariancja

OO    OO

d²x = ^ /

-oo    0

jest drugim momentem zwykłym rozkładu wykładniczego, skąd a — y/2/X. Obliczamy

Pr(\X-m\ > 3a) = 2Pr ( X > j = e“^3v/2

a więc nierówność (2.4.10) jest dla tego rozkładu nieprawdziwa.

Rozkład

lognormalny

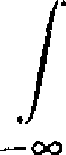
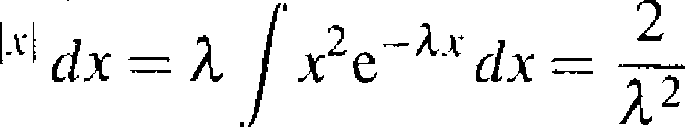
0.01437,

Z rozkładem normalnym związany jest rozkład lognormalny. Zmienna losowa X przyjmująca wartości dodatnie ma rozkład lognormalny, gdy jej logarytm ma rozkład normalny, tzn. lnX ~ N(m,cr). Oczywiście Pr(X > 0) = 1 i dys-trybuanta wyraża się wzorem

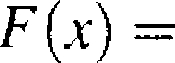
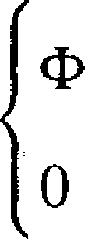
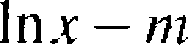
a

dla x > 0, dla a < 0,

gdzie 4> jest dystrybuantą rozkładu N(0,1). Gęstość rozkładu lognormałnego jest przedstawiona na rysunku 7.