036

36

2. Zmienne losowe

Ponieważ skok w zerze F(0⁺) - F(0) = 1/2, a całka w przedziale (-00,0) jest równa zeru, to

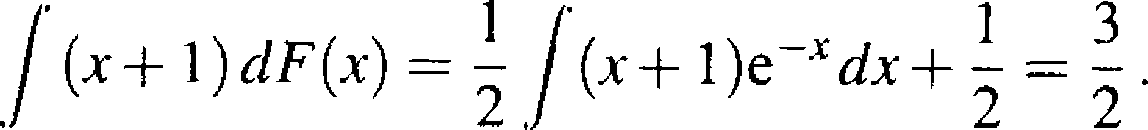
o

2.2.2. Wartość oczekiwana

Wartość oczekiwana zmiennej losowej, zwana też nadzieją matematyczną, wartością średnią lub przeciętną, należy do podstawowych pojęć rachunku prawdopodobieństwa.

Definicja.

Wartością oczekiwaną zmiennej losowej X o dystrybuancie F jest liczba oznaczana jako EX i określona wzorem

co

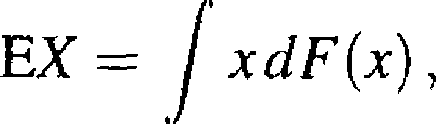
(2.2.2)

o ile całka we wzorze (2.2.2) jest bezwzględnie zbieżna, to znaczy o ile istnieje całka

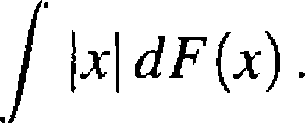
(2.2.3)

Twierdzenie 2.2.1.

Jeżeli zmienna losowa X ma dystrybuantę F(x) oraz Y = g(X), gdzie g(jc) jest funkcją przedziałami ciągłą, to

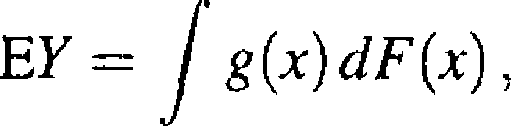
(2.2.4)

o ile całka (2.2.4) jest bezwzględnie zbieżna, tzn. o ile istnieje

oo

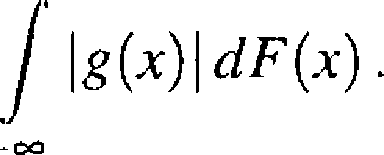
Twierdzenie 2.2.1 i wzór (2.2.4) jest bardzo użyteczny, bo pozwala na obliczenie EY bez znajdowania rozkładu zmiennej losowej Y.