135

135

Odpowiedzi i wskazówki

6.2.5.    Łączymy trzy pierwsze klasy oraz łączymy dwie ostatnie klasy, co daje r = 5. Zatem

P\=J2    (0.35)*(0.65)^10_t = 0.26164,

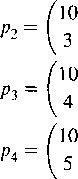
j(0.35)³(0.65)⁷ = 0.25222,

j(0.35)⁴(0.65)⁶ = 0.23767,

j(0.35)⁵(0.65)^s =0.15357,

Ps = ¹ - {P\ + P2+P3+P4) =0.0949.

Ponieważ y² = 2.15625 < 13.2767 = Xa> ^W*9^{C n}*^{e ma} podstaw do odrzucenia hipotezy, że generowanym rozkładem jest rozkład dwumianowy z parametrami n = 10 i p = 0.35.

6.2.6.    Szacujemy X=x, stąd 3 stopnie swobody, y² = 5.85 < %„ = 7.8147, a więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest Poissona.

6.2.7.    Szacujemy X = x, stąd 4 stopnie swobody, y² = 2.86 < Za = 9.4877, a więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest Poissona.

6.2.8.    Łączymy dwie ostatnie klasy i szacujemy X = x, stąd 3 stopnie swobody, y} = 0.99 < Xa = 7.8147, a więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest Poissona.

6.2.9.    Jest 1 stopień swobody, y² = 0.36 < y² = 2.7055, a więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest jednostajny na [0,1].

6.2.10.    _Pj = 1/3, 2 stopnie swobody, y² = 2.78 <    = 5.9915, a więc nie ma podstaw

do odrzucenia hipotezy, że rozkład jest jednostajny na [0,3].

6.2.11.    2 stopnie swobody, y² = 2.89 < y² = 5.9915, a więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest N(0,1).

6.2.12.    2 stopnie swobody, y² = 161.3 > y^ = 5.9915, a więc odrzucamy hipotezę, że rozkład jest N(—1,0.5).

6.2.13.    Szacujemy dwa parametry, stąd 3 stopnie swobody, y² = 2.91 < *2 = 7.8147, a więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest normalny.

6.2.14.    Szacujemy X = 1 jx, 8 stopni swobody, y² = 8.31 < y² = 18.1682, a więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest wykładniczy.

6.2.15.    Łączymy ze sobą klasy o numerach 7 i 8 oraz 9 i 10, otrzymując 7 stopni swobody, n = 138, a = 0.02, y² = 18.34 > y² = 16.6224, a więc odrzucamy hipotezę, że rozkład jest wykładniczy.

6.2.16.    Ponieważ n = 60, y² = 4.4 < y² = 9.4877, więc nie ma podstaw do odrzucenia hipotezy, że rozkład jest jednostajny na [1,3].