71 (156)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

201

d| Do zespołu Krysi i Uli dwie siatkarki można dobrać na * | sposobów. Pozostałe osiem dziewcząt nuiZna podzielić na dwa czteroosobowe

zespoły na ₍ |: 2 sposobów [patrz rozwiązanie punktu a) I. Zatem liczba szukanych podziałów jest równa j *^ | | j | :2 (=15751.

&) Do zespołu Krysi trzy siatkarki można dobrać na ¹ | sposobów. Gdy zespół Krysi jest juz skompletowany, do zespołu Liii trzy dziewczyny

mo/etny wybrać na . j sposobów. Pozostałe cztery dziewcząt utworzy trzeci zespół. Liczba szukanych podziałów jest równa | ^ • j ^ |

698. Na 35 sposobów. 699. a) 72.9; b> 90.

701. a)30240; b) 6720.

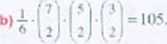
Rozwiązanie, b) k.i/da permutacja zbioru .4 jest ośmiowy razowym ciągiem. Trzy miejsca w tym ciągu dla liczb 1,2.$ można wybrać na j ^ | sposobów i każdy wybór trzech miejsc w sposób jednoznaczny określa którymi wyrazami ciągli są liczby 1. 2. 3. Po wybraniu miejsc dla liczb 1, 2, 3. pozostałe pięć liczb można spcrmulować na 5! sposobów. Zatem szukana liczba pcrmutacji jest równa J ^ | 5! (=6720).

702. Hj K40; b) 121X1.

703. 70 dróg.

Rozwiązanie. Zauważmy, że aby przejść z punktu (D. <0 do punktu <4. -ii należy wykonać X „kroków": 4 w prawo i 4 do góry (kroki wprawo i do gary mogą być wykiwane w dowolnej kolejnościZatem liczba dróg prowadzących i punktu (0. I>) do punktu (4. 4) jest równa liczbie ośmiowy razowych ciągów, którego cztery wynizy są równe 0 (kroki u />/i/irol i cztery równe I <kroki do góryI. Cztery miejsca a¹ ciągu ośmio-

wyrazowym dla wyrazów równych (I możemy wybrać na

sposohow. Zatem liczba szukanych dróg równa jest

704. W siedemdziesięciu.

Rozwiązanie. Ka/de dwie przecinające się przekątne danego ośmiokąta są przekątnymi [icwncgo czworokąta, którego wierzchołkami sit cztery wierzchołki ośmiokąta. Zatem liczba punktów , w których przecinają się przekątne, jest równa liczbie czworokątów, który ch w ierzchołki są także wierzchołkami danego ośmiokąta. Liczba tych czworokątów jest równa liczbie c/teroełementowych podzbiorów zbioru wierzchołków danego

wielokąta, czyli ^S I

705. a) —: b) 0.7. 706. ■?-. 707. 0.375.

708. a)0.54: b)0,58: c)0.7; d) 0.3. 709. a) 0.25: b) Ił. 15.

710. a)ii.. - zbiór'uporządkowanych par (A, ni takich, ze k e 1’ii/ie U; lub krócej: 12,, {</:.«): ts LT| i /z •“ ll»). 0.3:

b) ii. - zbiór uporządkowanych par (k. nl takich, że k. n e U.- lub krócej: ii. | (»'.. n): k. n c I 0.25;

c) ii. - zbiór uporządkowanych par (k. n) takich, że k. n G Ui lub krócej: ii, = | (k. n): k. n <z U| i k *n\, 0.3.

(poziom io \:, r oiv. ) ii zbiór wszystkich dwuelcmentowych podzbiorów zbioru Ui lub krócej: ii - j |A.w}: k. n <= U| a k / »i|. 03.

711. a) ii - zbiór dwuwyiazowych ciągów o wyrazach należących do zbioru (1.2.....6} (lub i2 zbiór dwuwy razowych wariacji z powtórzeniami zbioru (1. 2.....6| >: b) <L 11. (2. 2). (3. 3). t4. 4). (5. 5t. (6. (0.(1. 2). (I. 3). (I. 4k (1. 5). (I. 6). (2. 4). (2’. 6). (3. 6);

^{c,m, =} l8* ^m,=ł-

712.

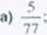
Rozwiązanie, a) Niech b oznacza zbiór uczniów tej klasy Korzystając z wykresu, obliczamy liczbę uczniów: | K | 2+0+8+4 + 2 Przyjmijmy. ze zbiorem zdarzeń elementarnych ii jest zbiór par (o. b). gdzie u. be tć i a*b. Wobec tego I ii I = 22-21.

I.iczba uczniów, którzy uzyskali ocenę co najmniej bardzo dobrą, jest równa 4 -i 2. Zatem 1. 11 = 6-5.

M t-

1/11 _ 6-5 _ Jj_ iii 22 21 “ 77-

713.

435 . 189!'

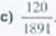
714.

6000

22.