63 (177)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA 193

552.

ii

V,

l+COStt

gdzie V'i objętość sto/ka ściętego.

553. Stosunek objętości: 1:2. Stosunek pil: t4n4 I):(4rt + 4i.    554. Pole: 2iHa+b)Ui+2c). Objętość: nab(.a+2c).

555. 5rc»\    556. Objętość: 4rr. Pole: 2/n-JJ + 3).

557. Objętość: 32n. Pole: 8>/3il i -J'1 i.t.

Rozwiązanie.

Niech H oznacza bryłę rozpatrywaną w zadaniu, czyli bryłę powstałą /. obroni trójkąta KIM wokół prostej KM. Obliczamy objętość i pule powierzchni bryły li rozważając dwa sto/ki: S, - stożek o promieniu podstawy r i wierzchołku w punkcie K oraz S> - stożek o promieniu podstawy /• i wicr/cholku w punkcie M.

Objętość Vj» bryły II jest równa różnicy objętości stożków S, i S_:. czyli:

V’„ =-i-ffr²(8 + /i)-yTr²/ł = -|ffr²+^-.Tr²/j--jTr²/ł = ^-.T/-². Zatem do obliczenia objętości bryły l< potrzebna jest jedynie długość promienia r. W trójkącie Ml A' sinftO⁰ - -7. —- = -7. stąd r = 2-/J. a więc    = $2b.

Pule powierzchni ł'_A bryły H jest równe sumie pól powierzchni bocznych stożków Si i 5%. czyli Pu = .tri 1- .trr-4 = It^MI + 4).

Korzystając / nr. Pitagorasa obliczamy najpierw wysokość It. a następnie tworzącą I. W trójkącie Ml.jV Ir 4* -ilj})² =4. stąd It = 2. W trójkącie KL\ / =(.8+ 21* +i2^3r = 112 = 16-7. stąd l = Ayfl. Ostatecznie /\,= 2;ZyfS(A fi + 4) = 8^3(1 -t    )t.

558. 52n.    559.

560. Objętość: r-|j==r/r. *°*^e powierzchni: -yj-Jl.

561.    (gdy trójkąt ABC jest OStrokątny i. -My tedy trójkąt ztBCjest ro/Wartokąlny).

___    1    3 (lg^-lgBllj:aijr/ł    t    3 sin crsin. 2 sin tf cos// j |

>    L⁼>    ij

563. 2xa

3 sin ' //sin ~ y

3sin*{/f+ył

565. a) 3.5/ru*’:    b) 2j?xa²:    c)6-JJrra².

564.

SylO.r 15 ’

566. jn.

567. zr<r' sin Zzt I -t- cos//).

Rozwiązanie.

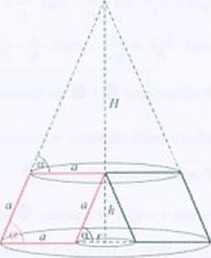
Objętość V bryły powstałej z obrotu rombu jest równa Vj - V_: - V\, gilzie I j. \ V, są ohjęlościanii stożków o promieniach równych odpowiednio u t r. a. r i wysokościach równych odpowiednio h t //, H. It.

V = i.Ttu-i r)²{/i+ H)--j-ti²lł -i*^,r-/i = ~-/r|i,/ + r)*t7i+ //)-u²tl -;^:/r| =

= yTi«/*/n- r²ll + Itirilt + // )|.

Łatwo obliczamy r, It oraz //: r - ucosrr. h = nsituz, // = otsa. Wobec lego: sin a + a' cos* <r tgr/ -1- 2a¹ cos >/< sin a + tger>| =

= ~xa'(sinu t cos* tr —'•* + 2 .sintteos/z + 2cosO'-^slll -^/-j =

3    cos a    cos er

- i r u 'l sin // 4- sin a cos a r 2 sin er cos « + 2-in a) - o ‘(3sin a l 3 sin //cosec i = tu ’ sin /*( I 4 cos cc).