66 (165)

196

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

612. -141 cnr (ramkę należ) /.butli>wać / dwóch części u długości 21 cm i dwóch części o długości 29 cm i.

613. 12 cm (bok kwadratu: 3 cm) i l(» cm (boki prostokąta: 2 cm i 6 cm).

Rozwiązanie, i długość boku kwadratu, y. 3\ długości boków prostokąta.

Suma pól otrzymanych czworokątów /' = i + 3y\ Wiemy, że 4v r Xv = 28. stąd mamy a 7-2y. Możemy teraz wyrazić pole /’ za pomocą zmiennej y: l'iy) i7 - 2v)' t 3v\ gdzie y e l) = (I); 3.51. Funkcja /'tyl = 7y*’ - 2Xy + 49 najmniejszą wartość przyjmuje dla argumentu

^1U

\ =--^=y “2e /). Obwod prostokąta o bokach v i 3y jest równy Ky. czyli 16. Zatem drut należy podzielić na części o dług. 16 cm i 12 cni.

614. 40 cm i 32 cm.

615. l*rnstoką( jest kwadratem o boku 4 cm; pole figury: 8ff+ 16 cm^: ( /’(il v² + 4(2 - 7>t + ló.T. »€(0;8). ,v długość jednego z boków prostokąta ).

616. Długości boków trójkąta: 6 cm. ó cm. 6y2-v3 cm I IH\) = il2.» -\² gdzie i e (0; 12). a - długość jednego z boków zawartych w ramionach kąta o mierze 30⁴ ł.

Wskazówka. Po wyznaczeniu długości boków zawartych w ramionach kąta o mierze .W - długość trzeciego boku można znaleźć obliczając długość jednej z wysokości, a następnie dwukrotnie korzystając z. nr. Piiaiiorasa.

617. x = 2. pole trójkąta: -J5 cm* (/Vwi-»)=—~(3a‘-I2.T + I6). a€ (0:4) ).

•I

618. 15 cm.

Rozwiązanie, a. h - długości podstaw, c - długość ramienia trapezu.

Sinus kąta ostrego trapezu jest równy -j-. więc długości wysokości jest równa -je. Pole trapezu /’ - 0,5(ri+6)- |e.

Wiemy, że a * h i Ir =60. stąd <j + /z=60-2<\ Możemy teraz wyrazić pole /’ w zależności od długości ramienia:

ha - <30-r)-~c. gdzie c€ l)=i0: 30). Funkcja /’tr) = ~jc" największą wartość przyjmuje dla argumentu « _H = 15 e I).

Zatem ramię trapezu o największym polu ma długość 15 cm.

619. Długości boków prostokąta: 3 i 4.

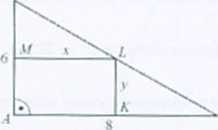
Rozwiązanie. Pole prostokąta P = ty. Szukamy zalc/ności między \ i y. Z podobieństwa

trójkątów ABC i KHl. matny = stąd y = 0.75(8 -a). Możemy teraz wyrazić

pole /'jako funkcję zmiennej s: P{n 0,75x(8-,v). gdzie re l) = (0; 8). Największą wartość tunkcja P przyjmuje dla argumentu \_u = 4 e /). Zatem jeden z boków prostokąta powinien mieć długość 4. a drugi 0.75 18 - 41 = 3.

620. 70cm x 105 cm ( Pole prostokąta (w m^:): Pi\) = l.5vfl,4- r). gdzie r jest długością boku prostokąta równoległego do podstaw trapezu i .re 10: 1.4)).

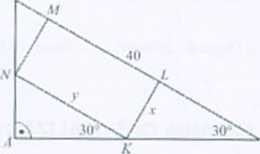
621. Długości boków prostokąta: 20 cm. 5v3 cm.

Rozwiązanie. Z trójkąta ABC mamy |.4ft| =20^3, z trójkąta KHL mamy A‘//| = 2t.

Z trójkąta AKN mamy |zlA'| = -^-. 2v + —= 20^3. stąd a - j——. Pole

prostokąta: P = xy = -^^<4(>4 '^M . Funkcja Ply) = (-y ² + 40y). gdzie y g i U; 40)

największą wartość osiąga dla argumentu y = 20 e (0: 40). Zatem największe pole ma prostokąt o bokach y=20 i i = 5^3.

622. •)/’u) = --|.t² + 2.r. b)P_lwl(l.5)= 1.5.

Wskazówka. /\wvv = P\ABC~(P.\n*:+P\uąs + P.\nvs^l-

623. 2. 624. 2^3-3.

625. Czworokąty o przekątnych równej długości i przecinających >ię pod kątem prostym.

Wskazówka. Wykorzystaj w/ór na pole czworokąta: /*=0.5/»</.sinu. gdzie p, </ - dług. przekątnych cz.wotokąla. a - kąt między przekątnymi.