57 (221)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

187

493. 5>/7.

494. 27/]?.

495. 45".

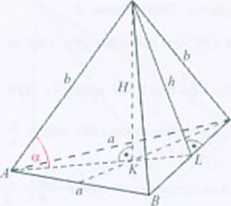
Rozwiązanie. Pole powierzchni bocznej osłroslupa wyraja się wzorem 3•■^nh. Zachodzi

więc równość ~ ah =    ' . Dzieląc obie strony tej równości przez o otrzymujemy

■}h = -^—«. stąd h = 2LlSL_a Znajdziemy długość h krawędzi bocznej. Z ru . Pitagorasa

dla trójkąta LCW: h² =h² +(% I* = <4^a>² +(i)² =il_a*+1«- =ii_a^J = *«-.

2    6    2    36    4    36 V

st.Hl h = ^j-a. Obliczamy długość odcinka AK. Odcinek AL jest wysokością trójkąta równobocznego ABC. więc I Al. |= natomiast

-2MU/L-J ₌VI

V6 V2

I AK l= -r- I AL I- —r~. W trójkącie AKW: eosa    -----

3    3    14 HI Jh J? 2

. stąd » = 45 .

496.    6sin«t3-4siit“ar).

Rozwiązanie. Dane: 5' - pole powierzchni hoc/nej ostrosłupa. 2n - miara kąta pomiędzy wysokościami ścian bocznych. Trójkąt EDW jest równoramienny, więc IZAU/d = a. Końce

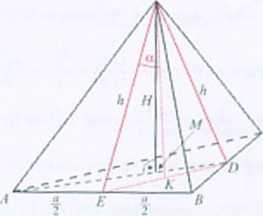
odcinka ED są środkami boków trójkąta ABC. zatem l/./>l = y. więc l£KI = j.

\£K\

W trójkącie EKW sina • yf^r\y\~'^’ n = 4/rsin<Ł Pole powierzchni bocznej ostrosłu

pa jest równe ^nlt. zatem .V - ~nh = 6/Tsinrt. a stąd h -    Obliczamy krawędź

podstawy ostrosłupa: a = 4/»sinzr= S sin a. a następnie długość odcinka MIK I ,V//> 1= i I AD 1=    = ^.S sinzz. Obliczamy wysokość ostrosłupa (trójkąt A//)H’|:

a).

„iiM„    .jEvs^w

497. 2

■Voistf

V3(l+«w<r)

o' J:3-4sin* " 498. Objętość: —2--

l2sinnrcos* "

u' V-3-4 sin ‘ a	. pole: a~	V3 + 3		3 11 , Vl2 I5sin* tt I
12 sin rz cos^1 et		4 co*^2® -sinrr		4cos‘ a ^ s'^n<3f J

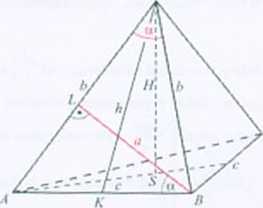
Rozwiązanie. Szkic rozwiązania. Dane: o oraz. (i.

I SPOSÓB W trójkącie BWL: b = -^. W trójk ącie KB W:

c = 2/>sin-2- = -''-sinIŁ    n bws-- - ^a- cos-^-. Wysi>kośc ostrosłupa wv/na-

2 .sm/r 2    2 sin« 2    '

czarny korzystając z tw. Pitagorasa

a Ji-4 sin ^: "

>. Pitagorasa: H = ——■=-—.

>/3sinzr

Do uproszczenia wyrażeń

trygonometrycznych stosujemy wzór sin«= sini= 2sin ycos-^f.

II SPOSÓB. W trójkącie lt\VL\ h =    ł-ilwo pokazać, ze IćAHIJ ~ O. W trójkącie

A PI.: c = d ^. Wysokość ostrosłupa oraz w ysokość .ściany bocznej wyznaczamy

ir

V3sinrrcos</    2sinrrcoszr

,    . •    , .    u-.    ,i <Jv3-4sin rr . iiV4-5sin‘a

korzystając z tw. Pitagorasa: //    -. h =» —f-—-—-

zostały w nawiasach kwadratowych.

Postępując w ten sposób otrzymujemy odpow iedzi, które zamieszczone