67 (164)

ODPOWIEDZI, WSKAZÓWKI, ROZWIĄZANIA 197

krawędzi AB).

Wskazówka. a - długość boku prostokąta równoległego do AB. y - długość boku prostokąta równoległego do AE.

Oblicz pole pięciokąta ABC DE |Ó4 dm'i. Wyra/, pole pięciokąta ARCDE jako sumę pól prostokąta o bokach długości a. y i w iclokątów pow stałych po wycięciu prostokąta <2i +4v-4X).

627. C=(4.0) ( j(.v) = Itr I(u4‘)(). .v6 R. ,t odcięta punktu C ).

628. /’=(!». 2) </(y) ^;-5y^J + 20y. y 6 (0:4). y rzędna szukanego punktu k

629.    /’=<2.2) (r/(.r) = A^:-4r + 8. as (0:+oo). r-odciętapunktuP ).

630.    Al = I—I. 2). polo: 8 (/*(*) = -0,5.v‘ 4r. a e t-8; Oj. \ - odcięta punktu XI I.

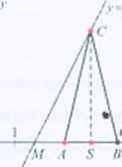
V - 2« - 4

631. 8.

Rozwiązanie.

S=(.r, 0) - środek podstawy trójkąta, gdzie a e <4; 6). Wówczas C=t.\. 1\ -4).

I AB| = 2-1 BS\ = 2(6-a>. I CS I = 2i 4.

Pole trójkąta /’= <1.5 • 2<6-a)(1» 4». Funkcja Pu> = (6-.vM2v-4i. której dziedziną jest zbiór /) = <4; 6). największa wartość przyjmuje dla argumentu >» -4 e D. Pole trójkąta / jest równe A4) = 8.

632.    Obwód trójkąta T. 12 ( Pole trójkąta P(t)=i 2 - r)t i + 8). gdzie v jest odciętą wierzchołka kąta prostego i »*= l-S; -2) i.

633.    8.

Rozwiązanie. <v. 0) - jeden z wierzchołków prostokąta, lezący na dodatniej pólosi O.X. Pozostałe wierzchołki prostokąta mają wówczas wspól-rzędne: |-v. 0) - drugi wierzchołek lezący na prostej o równaniuy=0. l *. 3- V) i (-.v, 3- »'j wierzchołki prostokąta lc>ące na danej para-boli. fioki równoległe do osi OY mają długość 3-.r*. boki prostopadle do osi f >)' mają długość 1\. Zatem obwód prostokąta jest funkcją zmień-

ncj v określoną wzorem ol.r| = 2(3-.r^;:) + 2-2i, gdzie .te /» = <0. v3l. Funkcja «(.0 = 2v^: + 4a +6 największą wartość przyjmuje dla argumentu Aj, = 11 />. a wartość ta jest równa <•( 1 i = S. Zatem największa wartość obwodu prostokąta o danych własnościach wynosi 8.

634. <2.0). (4.0). (4. -3). (2. -3).

635. /»=(•£.-J).

636.    a) Ca (-3. 10) lubC = (5. 26):    b)C = (l,2) ( /‘Ut = a' - 2r + 5. re K. i - odcięta punktu C ).

637.    b) /’(f)--0.5r + D.5/+ 10, t€ (0.4); c| Najmniejsze pole: 4. wierzchołki: C = (0,5),/) = (4. 0); największe pole:    10^.    wierzchołki:

C = (0. 1.5). D = (0.5.0).

638.    Podstawa: 20 cm * 40 cm. wysokość: 15 cm ( /’ ia)= 240a - 8a*. te (0:25), r - długość hoku wyciętego kwadratu ).

639.    Ihostopadlościan o podstawie 10 cm < 15 cm i wysokirści 13 cm; objętość: 1950 cm'.

640.    V=-~tl' ( Pole P{(t) = - (hi² v3 + 1W<i, gdzie u jest długością krawędzi podstawy graniastoslupa i <?e(0;    ).

641.    a) Krawędź podstawy: 4 cm. wysokość: 4 cni < /'(./> = -^-l8.i - ,r). ac (0:8), </ - kraw ędź podstawy ostrosłupa );    b) objętość:    cm .

643. 6a/2.

642.    a) i. b) I4a/ó.