59 (198)

189

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

506. Pole:    3. Tangens: ^-\ga.

J>r

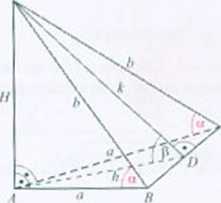
Rozwiązanie. Ściany AttWi ACW są trójkątami prostokątnymi. każda o polu 0,5«//. Ściana fl('W jest trójkątem równoramiennym o polu 0.5<ó. Ponieważ k > //. więc spośród ścian bocznych największe pole ma ściana HCW i pole lej ściany nalepy znaleźć.

W trójkącie A UW:    stąd // = alga. Odcinek APjesl wysokością trójkąta równobocz

nego ABC. więc li =~Ł. Obliczamy wysokość k korzystając z iw. Pitagorasa (trójkąt .(/.'U'): k‘-n'+h²= u² ig² a 4-^- =    = -^-(4ig²rr + 3). stąd k = -jj4ig~r/ +

Pole ściany PCW: P = ±<tk =    ^4ig-« + 3. tg//= ^    -j=iga = ^~Iga.

507. H.

<>

503. ^iŚL£lił.

COMT

Rozwiązanie.

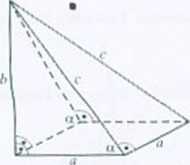
iźda ściana boczna ostrosłupa jest trójkątem prostokątnym. Pole powierzchni bocznej Iroslupa /’-2 -i-rrb + 2 —c/c -«(/>+r). ł/=algcr. r- ^.

nem /'= «< </tga + -    = «

^e    cos ar

2 sin r* + I

cos a

509.

!>' siii/^icus" « sin²

3 sin* <r

510

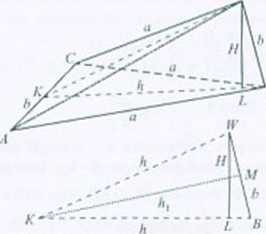
Rozwiązanie.

Ka/da ściana ostrosłupa jest trójkątem równoramiennym o podstawie długości b i ramionach

wiązanie.

da ściana ostroshi

długości a. Wysokość podstawy ostrosłupa ma długość h    -y = — J-Ue'^L -h~ .

więc pole podstawy P, < istroslupa jest równe: P,. = i- !>h = — \4a    Aby obliczyć wy

sokość ostrosłupa obliczamy najpierw wysokość li, trójkąta równoramiennego KB W:

h, =    - Ja~ -Ą^ =    . Porównując wzory na pole trójkąta A7MP

dostajemy równość -|/»W    ^W'|. a stąd // 2/tl    ■ Obliczenie objętości ostrosłupa pozostawiamy czytelnikowi.

-    -    V 2(4<i--/ri

511.

Wskazówka. Uzasadnij. Ze spodek wysokości ostrosłupa jest punktem równooddalonym od wierzchołków podstawy.

512.

Wskazówka. Środek okręgu opisanego na wielokącie jest punktem wspólnym symctralnych wszystkich boków tego wielokąta.

513.    i-/TT.

Rozwiązanie.

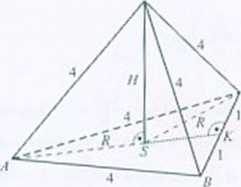
Przyjmujemy, że podstawą ostrosłupa jest trójkąt o bokach długości 4, 4. 2. Wobec tego wszystkie krawędzie lxiczne ostrosłupa są tej samej długości (równej 4). Na mocy tw. o ostrosłupach spodek wysokości ostrosłupa (punkt S) jest środkiem okręgu opisanego na jego

podstawie. Obliczamy długość wysokości AK trójkąta AHC: L-1A1 JlŚ oraz pole podstawy ostrosłupa: P_f, - -fi5. Obliczamy długość promienia okięgu opisanego na trójkącie ABC'

Korzystając ze wzorów na pole trójkąta możemy zapisać równość ~2-Vl5 = stąd

K = ~=. Wysokość ostrosłupa: H    objętość ostrosłupa: V ~Ppłl~^yf\\.