60 (198)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

190

514. ~^^L- ⁵¹⁵- Objętość: Rozwiązanie istnieje dla cre (0: ^S-).

516. 2-f*sin ycos/Igor.

Wskazówki. I Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie ostrosłupa (dlaczego?). II. Gdzie znajduje się środek okręgu ('pisanego na trójkącie prostokątnym?

517. +«*«■'tg/!.

518. Pole powierzchni całkowitej: (— r l)d' Objętość: -j-f a

519.

2 cos (i

Wskazówka. Spodek wysokości osuosłupa jest śmdkicm okręgu wpisanego w podstawę ostrosłupa (dlaczego?).

520.

Wskazówka. Uzasadnij, ze czworokąt Ki MN jest rombem.

521.

Wskazówka. Miary tych kątów są równe miarom kątów pewnego trójkąta.

522.

Wskazówka, Sporządź, taki rysunek osin.słupa, aby podstawą była jedna z prostopadłych ścian. Wysokość podstawy poprowadzona z wierzchołka kąta prostego, wysokość czwartej ściany i jedna z krawędzi bocznych tworzą trójkąt prostokątny.

523. Js^sficma*ina. 524. lub

525. a)-|V2; b) 6(76-1).

526. ^21iL

sin a L 2 J

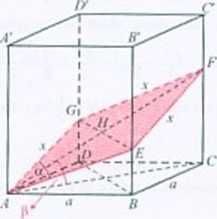
Rozwiązanie. Oznaczenia: </ - krawędź podstawy prostopadłościanu, .i - boku rombu,

/>- dłuższa przekątna rombu, fi- kąt. którego kosinus jest szukany.

I SPOSÓB Ponieważ FM 11 BO. więc l£GI = ujl.

7. nr. kosinusów dla trójkąta AEG: 2<t~ =2 r“ - 21" cos er, <i~ = a “(I - coso), stąd ■t~ = y - —■ Z Iw. ktbiiittsów dla trójkąta AEF: p~ - 2.r" — 2.v“ cos(l80° «) =

= 2x~ + 2a“ cos<r = 2jv“(I + cosff) =-r-2s—o ą-coszr). stąd p =

1-cosrr V l-coszr

_cos«__ aj2 _; /j-eos,r _ /tl-cusgWI-cosrt) _ M-cnsrrr _ Itl-cosor i._c„_s„

' l.\/'t p V l+cosflr y (I+cos a\( I -i os a \ ]j |__cos2 _a y _jin2 _a siiur

II SPOSÓB cosfi yyyy = Długość krótszej przekątnej rombu jest równą długości przekątnej pGtlsliWiy, witJC \v Utójfcyae AEH

527. -Ł^:ig«.

•ł

520. - V-^s-4cos*tf.

RCOSff

529. Pole przekroju: -^p-a². Tungeits: 2yfJ\

Wskazówka. Wykorzystaj nr. Piniyorasu i oblicz kolejno: wysokość ściany bocznej li. wysokość otrzymanego przekroju h_{. wysokość ostro słupa//. Otrzymasz h=^Ę-a. //