8 (1047)

138

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

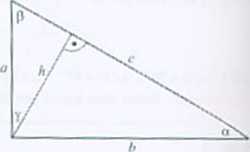
2.34 a) ig(ZBAC) «= -y. cos( A U AC) = y; b) IZ4SC1 = 60*.

Ro. ivM. arnc. a) lg(ZftlC) = n^r = ^ = 4- Z fu*. Pitagorasa dla trójkąta .AZIC: MO^;=8^:+6^:. Stąd 140= 10. cns[ZBAC) =

>zti>\ h •» 1.40 10 5

b) tglZARC) = 7§S = “V = TwięcIZ/łZiCI = 60*.

^,/,/ł| 2/3 <3

2.35 Przyprostokątne: —i ¹¹

•an/r ci»rt

prr.cciwprostc ikąlna:

- A_

Rozwiązanie. —■ = sin«, Stąd b --Ji—. — = cos«, stąd r =—-—= ‘‘i”^(l■ = ——--.

/» sin r/ c cosrr cosa suw? cos/?

Suma miar kątów ostrych trójkąta prostokątnego wynosi 90*. więc ft+ li-90 i /j=90\

Stąd wynika, ze r= a. — = cos y=civsr* więc u = ——.

a * ' eos<?

2.36 24^6.

Rozwiązanie. Pole trapc/.u: P = 2fLtlL. Jh - 2^6a. I AK | = ¹1 1 = ^ “ = a. tgo = . więc a =

- - - I AK I tg<?

wartość sinusa

Stąd otrzymujemy:cos^;rr= więc c<«tr= -=^-. tg/?= = —4= = -i-.

25 5 ^c cos O

Zatem P = 2 Jba = 2= 24-76.

tg??

	/6 N.
/u	ii__2s

3«

2.37 SOS.

Rozwiązanie. Pole trapezu: /’ = /i = 50/r. I KB I = \AB | -1 AK | a 70 - 30 = 40.

- tg22‘ - 0.404. zatem h = 0.404 ■ 40 = 16.16. Modemy teraz obliczyć pole trapezu: Pt 50/1 = 50-16,16 = 808.

22°

K 70

2.38 Promień okręgu wpisanego: \R. obwtki: yJlR.

Rozwiązanie. Oznaczenia: u - długość boku trójkąta, li - długość wysokości trójkąta, / -długość promienia okręgu wpisanego w trójkąt. Promień okręgu wpisanego w trójkąt równoboczny ma długość równą jednej trzeciej długości wysokości trójkąta, a długość promienia okręgu opisanego równa jest dwóm trzecim długości wysokości. Zatem r- ^-R.

Wiemy, R -Ąli i h = ^-. zatem/f = ~4ł^.Stąd otrzymujemy a = fili. Obwód trójkąta jest równy 3a, czyli 3^3 R

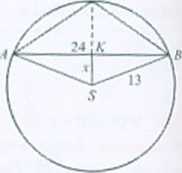
2.39 ‘)ft.

Rozwiązanie. Z ftr. Pitagorasa dla trójkąta SBK .»^; +12* = 13'. Stąd x = 5 ICA1 = ICS1-a = 13-5 = 8.

Pole trójkąta ABC: P =0.5 -M0I-IC%1 = 0.5 24-8 = 96.

2.40 yo//sin( 180" -a), a po skorzystaniu ze wzoru redukcyjnego (poziom rozszerzony): ab sina.

Rozwiązanie. Trzeci kąt ma miarę 180° - a, zatem pole P~ -^zj/>sin(l80° - a).

2.41 32.

Wskazówka. Wy sokość rombu jest równa średnicy okręgu wpisanego w romb.

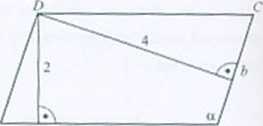
2.42 20.

Rozwiązanie. Wiemy, zc O 2<M 26=30. Ze wzoru na pole równoległoboku P-2a i P-Ab. więc © 2/z =4/>. Z układu równań O i 0 otrzymujemy 6 = 5. Obliczamy pole równoległo-boku: /^,=46=4'5 = 20.