6 (1275)

136 ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

2.12 45.

Rozwiązanie. Trójkąty są podobne, a skala lego podobieństwa jest równa j. czyli 4-Obwńd trój kąta n bokach długości 6, I0 i 14 wynosi 30.

Stosunek obwodów obu trójkątów jest równy skali podobieństwa, zatem obwód większego trójkąta jest równy 4-30= 45.

N .1 M

2.13 yfi. yfb, 3.

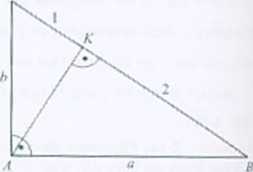
Rozwiązanie. Trójkąty AHK i ABC są pixlobnc {cecha kąt-kąt). więc stosunki odpowiednich bok.iw są równe: ^ ~ Stąd a = {b. Z podobieństwa trój-kątów AKC i ABC lub z Iw. Pitagorasa obliczamy długość drugiej przypnrsto-kątnej: b=i3.

2.14 |r>Cl=|(łi.

Rozwiązanie. Z Iw. Taksa wynika, że 7777-7 = Zatem I0CI =    = I6—.

lUJJI \AL>\    I2 4 i

2.15 |A7-|=7|.

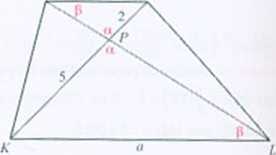
Rozwiązanie. Kąty trójkątów KLP i MNP mają równe miary tkąty KPI. i MPN - kąty wierzchołkowe, kary KU' i PNM - kąty naprzcmianlegle) więc trójkąty te są podobne. Jeśli trójkąty są podobne. to stosunki odpowiednich boków są

równe: -y ⁼ 7 • otrzymujemy a = 7.5.

2.16 14:17.

Rozwiązanie, k - skala podobieństwa wielokątów. Stosunek obwodów tych wielokątów jest równy k. Stosunek pól wielokątów podobnych jest równy k¹.    więc k =

2.17 64 cm^:, 36 cm'.

Rozwiązanie. * = y “ podobieństwa wielokątów. Stosunek pól /’, i P_: tych wielokątów jest równy kwadratowi skali podobieństwa, zatem -p- = -jy. Wiemy. Ze P₂ = P, + 2X. więc _y, ^ = yj-. Stąd otrzymujemy P, = 36. /\ = P, + 2K = 36+ 2X = 64.

2.18 2—J2.

*2 *•!

Rozwiązanie. Jeśli bok kwadratu ma długość u. to przekątna ma długość nV2 Musimy więc rozwiązać równanie nV2 + a= I. Rozwiązane otrzymamy wyłączając a przed nawias: a(%2 +1) = I, a następnie dzieląc obie strony równania przez. V2 + I: a = — *—. Przekątna kwadratu

ma długość a% 2

s'2+l

. Po usunięciu nicwymiemości z mianownika długość przekątnej możemy zapisać w postaci 2 - /2

2.19 75° i 105*.

Rozwiązanie. Przekątne rombu zawierają się w- dwusiecznych jego kątów, więc kąt ostry ma miarę 2a. a kąt rozwarty miarę 2łir+J0\

Trójkąt ABS jest prostokątny, więc o + a+ 15° = 90°. Stąd 2a=75^c. Zatem kąt ostiy rombu ma miarę 75". a rozwarty 105®.

2.20 13 cm.

każda z. nich na połowy.

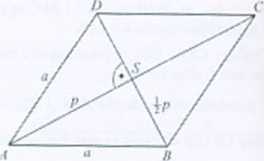
Wskazówka. Przekątne rombu przecinają się jkm! kątem prostym, punkt przecięcia dzieli

Rozwiązanie. p - długość krótszej przekątnej. Z tw. Pitagorasa dla trójkąta ABS a'=p^: + -L p-. Stąd a = ~p.

Szukany stosunek: ~

3 P    3 p    3