37 (316)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

167

163. 2cosa( I -cosa) ( = rg ^sin la ].

d~ cos^(45° - —)    dcos(45^<’-">

164. Pule: -— . promień: -—.

tgtt    sin 2«

165. 2>/l5.

Rozwiązanie. Oznaczenia: 2<i. h. r. fi - długości odpowiednio podstawy, wysokości poprowadzonej do podstawy, promienia okręgu wpisanego, promienia okręgu opisanego.

Wyrazimy r i R w zale/ności od a. Ir+<r - r4 «>•’. więc li — iiy/\5. Pole trójkąta P =    • 2n ■ a^\5 = ii J\J.

t    f-

Ze wzorów na pole tłójk^ta /‘ = -rUM/t + r).    ¹ z równości P*ir JlŚ otrzymujemy r=^~- 1 R= .

Wiemy, ze    + ^^-= ll.Stąda=Vl5. więc podstawa ma długość 2>/l5.

166. .1)

frsinr?

b>

/' sin «

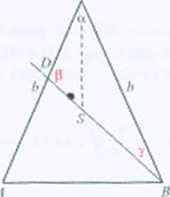
2(sin^ + l)" sin y Rozwiązanie, b) Trójkąt RCS jest równoramienny, odcinek SC zawiera się w dwusiecznej l^a ACH. więc y- 0.5rr. ji- I80* - (a + f) = 180° - 1,5<x Z tw. sinusów dla trójkąta BDC l> _ \um iim 1X0°-!_•;«) wn«*

_SUfl\_nR\ —hm<*—

sini 1X0° -l.5nr> sm1.5ff

^,67- w-

Wskazówki. I SPOSÓB. Skorzystaj z. tw. sinusów. sin2« sini a + u) = 2sin«cosrx li SPOSÓB Dwusieczna Mu ABC dzieli trójkąt ABC na dwa trójkąty, z których jeden jest równoramienny, a drugi jest podobny do trójkąta ABC.

169.

Rozwiązanie. Z nierówności trójkąta mainy jr+.v>a i )■ + ;>/» i * + t>c. Dodając le nierówności stronami otrzymujemy nierówność 2v +2y + 2: >0 + 6 + «\ a po podzieleniu obu stron otrzymanej nierówności prze? 2. dostajemy v +>• +z >0.5(o +b+c).

170.    tgZOIP    Stosunek promieni: I.

171.    sinZGM/a-^. KinZMAB=^-.

172.

S/ód

₁₇₄.    lub JatEn.

4    4

Rozwiązanie. Oz.n. c - długość trzeciego boku. u - miara kąta trójkąta lezącego naprzeciwko boku o długości KO.

Ztw,sinusów -fo* . = 2R. Stąd sinas-⁵^. zatem tf=ó0° łub a= 120®. sin u    2

Jeżeli tf=60°. to z nr. kosinusów Vi²=c²A-^fi¹ - 2c -L. Otrzymane równanie sprowadzamy do postaci 2c‘ - cR -    R² - 0.

Dodatnim rozwiązaniem tego równania jest c = ^    ^ .

Jeżeli 11 = 120°. to z. tw. kosinusów 3/r = c² + K² - 2c ■ -L fi (--!■>. Otrzymane równanie sprowadzamy do postaci 2c‘ + cR - JJ- A” = u

•    _—x ^1^17

Dodatnim rozwiązaniem tego równaniu jest r =-—^u—.

175. 1/10=8.

Rozwiązanie. Oznaczenia: 18(1 = 2*, \ZABO=2a.

'/. nr. cosinusów dla trójkąta ABC: O 36= l6+4r- lóicosa.

Z tw. cosinusów dla trójkąta AHA’: © 10= 16+.t' -Xi cosn.

Mno/ąc równanie © przez -2 i dodając stronami otrzymane równanie 1 równanie O. dostajemy 32 = 2r\ Stąd 2r = 8.