64 (177)

194

ODPOWIEDZI. WSKAZÓWKI, ROZWIĄZANIA

568. Objętość: 243n: pole powierzchni całkowitej: Sini I i -Jl).

569.

-Ti l3-4v^r7l

3

570.    2n.

571.    4xH" sin acostf(cos«-ł-II | =^A^,3siń2<Z(2sint? + sii)2«> |.    572.

573. 60° lub około# I* (sinus połowy tego kąta jest równy

\V ;l. i*óv/Ki. I. Dwukrotnie zastosuj tw. sinusów. II. Skorzystaj ze w/otu .on2a^: sintu t ot = 2sinutcosa.

574.

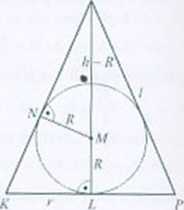
Ro:wi.-ic-:inie. Oznaczenia: r promień podstawy stożka. I - tworząca stożka, h wysokość stożka. R - promień kuli wpisanej w stożek. \'s - objętość stożka. V* - objętość kuli. P_r - |*>le powierzchni całkowitej stożka. I\ - pole powierzchni kuli.

+ rl

V_S :V_K=±xr¹h:jxR^y=± ^. Ą :P_K    +*rt):4rt²

r>    K

K |o- I	r~ -rrl
R-	R^2
Zatem	IKL\ _
	IA3I
— - r	-l, i
R

Należy udowodnić, że Vg :    = /’_s- : }\ . czyli, ze

stwierdzamy, że należy dowieść, że    i /.

A

Trójkąt KLS jest podobny do trójkąta A/A'.S'(ri.v/kj/;J;l. Zatem    czyli Z.    IVzekszt.il-

IAJjI lAfu I '    I h A'

ih.

R

575. -k.

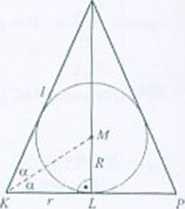
ftuzwiąranio. Oznaczeni,i: r - promień podstawy sto/ka. / tworząca Stożka, h - wysokość stożka. U - piomień kuli wpisanej w stożek. Pr - pole powierzchni całkowitej stożka. /’/ - pule powierzchni kuli. Należy obliczyć COs2i/.

Wiemy, ze Pr - 2P_K. *r + xrl = 2-4.tU\ r^! + rl = Kir. O I + L = 8 [$- f.

W trójkącie KLS y = cos2r/, stąd O ■- -—. W trójkącie ATM 0— te o. l*o pocłsta i    r cos.O’    r

wicniu 0i0 do równości O otrzymujemy równanie lrygonotuctiycz.ne I i -

cos 2zr

8 tg * a.

Przekształcamy: cos2# + I = 8 tg* a - cos2or. cos² rż-sin² a r I = ,s--*^lłl ^a -(2eos² u - l i.

cos' <1

_ ł* l-cos* a cos* a

f =4(1 - t)(2t - 1 k "r 12/ +4 = 0. (3/ 2>' = 0, stąd / = -=. Zatem cos2rr= 2cos'ł/- I 2/-I    4".

2 cos' u - S ■ ¹ u • i 2cos~ u -1). Niech t = cos.¹ a. Wtedy 2/ = S-—(2/-I), cos"a    '    ’

576. “ - lub

S

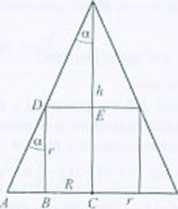
Ro.*'.vin:nnio. Oznaczenia: r - promień podstawy stożka i wysokość walca), h - wysokość stożka. K promień penistawy walca, V. objętość stożka. \'» - objętość walca.

Ks' ^:VM' =-{^trr¹lf.nR^:r = -ZĄ-. Wiemy, że    . stąd O—” 8. W trójkącie ABD

3    3 AT*    3/?*    ^3    A «

\£a - ZZJL - \JL_t Maj Ł | - tga czyli 0 ~ —•— . W trójkącie DLS tg«

r    r    r    a I—Igłi    /i—r

$tą.d    = ——. czyli    ——. Podstawiając © o(rzvmujemv ©•£■ = —L.₍ __!—.

R tgor    R R ty.tr    ³    R ig a l-tgar

Podstawiamy © i © do równości © otrzymując równanie O —-—I —-t—¹— | = s.

1-lgC^lga l-tg«J

Mianowniki ułamków w równaniu O nie są równe zero, gdy/.O -: tg«< 1 (nierówność tg«> I) jest oczywista, ale również Igr/ =    = |i.

Przekształcamy równanie ©: ----¹—-_t—- X. -'■-_r-X, Stgrzt I tg«V = l. XtgV I6tc*tf+8tg« 1=0.

1-tgr/ tgrt(l-tgo-)    tgatl-tgrtr

Niech t - tgtx. Wówczas © 81' - lor + Sr - I =0. Jednym z rozwiązań równania © jest r, = 0.5. zatem dane równanie zapisujemy w postaci </-0.5)<8r- 12f + 2) = 0. Pozostałe rozwiązania: r, =- ^. /i = -⁺^. / = tg«< 1. więc ostatecznie tgo-= vd. |„|, tg«--L.