55 (233)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

185

477. 48 cm'.

478. 8^4.

479. a) 45":

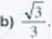
480. Objętość: ya^igct

Pole:    .

OB(I

IV

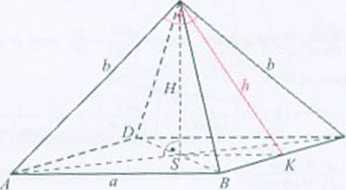
481. Objętość: 'ó>/2. Pole powierzchni bocznej: 36-73.

| Rozwiązanie.

Ziaważnty, że trójkąty ACW i Ad) są przystające, gdyż. są to trójkąty prostokątne rów-iorumienne o tej samej przeciwprostnkątnej. Wynika stąd. A* b ■ a. Korzystamy z tw.

Pitagorasa. W trójkącie KCW a~ = (4fi" +    stąd a = 6.

W trójkącie SKW    --3 ² + //². stąd tf = 3>/2.

Obliczamy objętość i pole powierzchni bocznej ostrosłupa:

V={,r// = W2. /V 4 loA = 36V3.

482. 56.

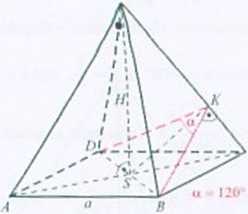
Rozwiązanie.

Przekątna podstawy ma długość ty/2. Obliczamy długość odcinka SK (trójkąt BKSy.

korzystając z iw. Pitagorasa (trójkąt SCK): \ KC\² = (łjl)¹ -l-Jb)². stąd I KC1= 2^3. Zauważmy, ze trójkąty SCK oraz SKW są podobne (cec/ui U. gdyż są to trójkąty prosto*

kątne oraz IZCSK1»IZSWK1). Zachodzi więc równość 7777 = 7777. czyli =

IaC I \ut% I    y6

stąd // = 3. Objętość ostrosłupa: V - ~o'll = 36.

483. ^S³igmi-tg²flr>.

Rozwiązanie. .SzAir rozwiązania. Oznaczenia: <1 - krawędź podstawy, /; - wysokość ściany bocznej ostrosłupa. Wiemy, że .V =~ah oraz tgcr=-^-. Wyznaczamy a i It. a następnie obliczamy wysokość // ostrosłupa. Otrzymujemy: u = ^4S tg <r, h =    // =

484.

-I

tg'«

485.

Ó^llg* ft-t

Wskazówka. Patrz rozwiązanie zadania 482.

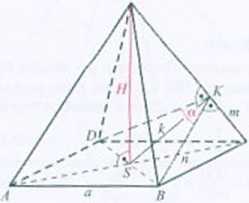
486. j/łⁱUg²f-l). Rozwiązanie.

ajl

2

tg^ = f. stąd * = -^L. W trójkącie SCK: n^: - k^:+m². czyli m' = -*il--«1_.

*2    4    2tgy    2 W*

/T /tg* ^-|

stąd w = —^ - ■ —-^-. Trójkąty .S'CA oraz SA'tV są podobne {patrz rozwiązanie

tg^;r

?“*■ «** ^S*^J •

zadania 4821. zatem Objętość ostrosłupa: V = yo¹ll =-|7/ \tg“ y-l).