5 (1397)

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

135

2.5 ayfl.

Rozwiązanie. 5u - długość przcciwprostokątnej. h - długość dnigiej przyprostokątncj. t- długość środkowej poprowadzonej do dłuższej przy prostokątnej.

Ztw. Pitagorasa dla trójkąta ABC mamy «^:+6*=(5«)'.

Stąd b^! = 25n^:-ti^:- 24n\ więc b-t24.r- = >4 -    = 2\(*t.

'Al 1 = 0.56 «>6fl. Z iw. Pitagorasa dla trójkąta ABC mamy i^!=n^: + (&r)~. Stąd otrzymujemy s = ilu.

2.5 II). 4^85.

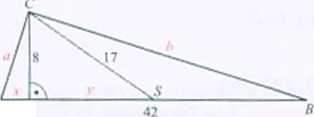
Rozwiązanie. Z tw. Pitagorasa dla trójkąta KSC 8' ♦ y = 17‘. stąd y = 15. Punkt Sjest środkiem boku AB. więc i = 21 -y=6.

Ztw. Pitagorasa dla trójkąta AKCobliczmy a = ID. Z tw. Pitagorasa dla trójkąta kBCobliczmy />= 4^X5.

.< A

2.7 7-|. 7i. 9.

Rozwiązanie. Środkowa poprowadzona do podstawy ma długość ^f). Z nr. o irodkowyc h trójkąta |A.'.*>] - 4-|AT<r| = 3. Z nr. Pitagorasa dla trójkąta AKSotrzymujemy MSI = 5.

|AS| = *\Al\. stąd |Mj = 7.5 = |JW|.

2.8 M6I=I0. Ma«4v/i3.

Rozwiązanie. Z nr. a irodkowydi trójkąta MSI =-j-1.4/. I = 6.

U5Sl = j IMI=8, ISA! = | l/iA'I = 4. Z nr. Pitagorasa dla trójkąta 4/łS Mfil^:=6^J+8^ł. Stąd 1461= 10.

Z nr. Pitagorasa dla trójkąta ASK L4AT = f>'’ +4*.

St*l MAI - 2/l 3. MCI = 2 MAI = 4/f3.

C

2.9 2 i 3.

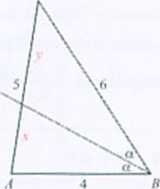
Rozwiązanie. — - 4 (fkarzYStaliśitn z fu . o dwusiecznej kata u trójkącie) i .» i v=5. y o

Rozwiązaniem otrzymanego układu równań jest para t=2 i y=3.

C

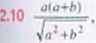
b(a+h)

y/skazowka. Skorzy staj z nr. o dwusiecznej kata trójkąta i ; tw. Pitagorasa.

2.11

Rozwiązanie, a) Trójkąty AKC i BLC są prostokątne i mają wspólny kąt ostry (kąt cf\. ■ięc są podobne (cecha kąt-kąt).

6) Trójkąty LAS i BKS są prostokątne i mają kąt ostry o tej samej mierze tkąt fi), więc >ą podobne (cecha kąt-kąt).

e| Z podobieństwa trójkątów AKC i BLC mamy ~ = trójkąty ABC i LKC mają wspólny kąt (kąt a). więc są podobne (cecha hak-kąt-hok).