68 (159)

198

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

644. Kwadiat o boku 15 cm ( /'u) 2tH-\ t- 300. i e (0; 30). \ - długość jednego z. hokó\v prostokąta ).

645. 250* cm\

646. Sionek o wysokości 13 dm i tworzącej 4.5 dm ( V</ł» = 4n<3/i—hr). /ie(0;3>. h - wysokość stożka ).

Rozwiązanie. / długo& płomienia podstawy, h - długość wysokości, (<-h - długim¹ tworzącej stożka.

Objętość stożka V - ' ~r'h. Z tw. 1‘iiagorasu If + r =(6 li)~. Stąd r = 36 - I2/i. Objętość stożka możemy więc wyrazić za pomocą długości wysokości stożka: VWil --jjr(3b-l2/i)A, gdzie heD = (Q; 3). Funkcja V(h) = -4nJt^: + 12rJi największą wartość przyjmuje dla argumentu li_u= 1,5. Zatem szukanym stożkiem jest ten. którego wysokość ma długość 1.5 dm. a tworzącą długość 4.5 dm.

647.    486iccni' (Objętość V(«)=24rt<0-rri</. gdzie o jest połową długości podstawy trójkąta i oc l0: ‘>j I.

648.    3ft.

Pt:*tnij tntnntupa plnncsytuĄ urmtntpęą /ego m\*otair i    prze: irnJijJmiA

1/ju yi/.-i ptuhurn i'

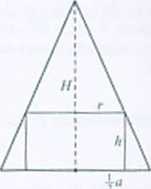
649.    Długość promienia podstawy walca: -j-o.

Rozwiązanie. Pole powierzchni bocznej walca: P-2wh.

Korzystając / podobieństwa odpowiednich trójkątów, otrzymujemy równość -jj -    . z której wyznaczamy /i =    -2r). Możemy teraz wyrazić jkiIc powierzchni bocznej walca jako (unkcję długości

promienia podstawy: !‘\r)=    -2n. gdzie r€ D=(0; ~m.

Funkcja kwadratowa P(rt = ~~(-2r^: + ori. największą wartość przyjmuje dla argumentu <z«* = -jo e />. zatem szukana długość promienia podstawy walca jest równa -ju.

650. Długość krawędzi podstawy graniasiosłupa: -i-o.

651.    Objętość prostopadłościanu: 225 (długość wysokości: 3V3. długości krawędzi podstawy: 5 i 5»3).

652.    I0 cm x 24 cm.

653.    Długości krawędzi podstawy: 15. 20. 25. Długość wysokości: 2.5. ( Pole powierzchni graniasiosłupa /’(*) =-ł8.v’+ lSO.t. gdz.ie 3» jest długością kndszej przy prostokątnej podstawy graniasiosłupa i .i e (0; 6) j.

Wskazówka. Pr/eciwprostokątna dolnej podstawy graniasiosłupa zawiera sic w średnicy podstawy stożka.

654. Najmniejsza różnica: 2.    655. 12+20+24.

656. o<.no (oi =-3 ).    657. Ciąg o ilorazie -0.5. Wzór na wyraz, ogólny ciągu: o**—-—-.

t-2)"~

658.    2.3 mm (/(.) = H\ - 2.5F + 2U- 2.25)^: + <v- 2>' = 5.v* - 23« +-^ ).

659.    700krów. zysk: 1470 z.ł t Tin) = (3 - 0.tXl3ntt400 + n) - 1200 + 1,8»i - 0,003m\    N.. 400 + n - liczba hodowanych krów ).

660.    a) V(n) = n" - 20n + 230; b) po upływie 10 min (1301); c) w 2^l* min.

661.    -I ( /(n)=a^ł+2n-1. gdzieri€ R ).

662.    p=-l.

Rozwiązanie. Dla każdej wartości parametru/> jednym z. rozwiązań danego równania jest liczba -2. Drugie rozwiązanie /-jest największe wtedy i tylko wtedy, gdy suma liczi) r oraz -2 jest największa. Suma ta jest równa st/o - /»' - 2/» {skorzysliiliśmy ze wzoru Virle ot. gdzie p e R. Funkcja > największą wartość przyjmuje dla argumentu p*=-\. Zatem szukaną wartością parametru p jest -1.

663.    Nie istnieje taka wartość parametru p I suma pierwiastków: .d/»i = -2/»’ + 4/», gdzie/«e (-*•; 0)u(l,5: +«■>>).