56 (225)

136 ODPOWIEDZI. WSKAZÓWKI. ROZWIAZA

2    a

487. 2,1

MII* «cos«

Ad

i ^TT-

sin a sin <r sin 2 a

Rozwiązanie.

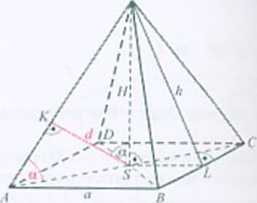
Zauwa/my na wstępie, ze IZKSM - 90° - \ZASK\ = 90' - CM)- - a) = a. Jeśli długość krawędzi podstawy ostrosłupa oznaczymy prze/ a. to:

\AO = aj2, \ASl=^-. LS/.I =±. Trójkąt ASK: s\na = ^ = -^ = ±£L, stąd

MSI ₀j2

,i    Trójkąt ASW': eos« =7^7 - -77. stąd // = ——.

ISWI II

sina Tnijk.it SLW:

cus a

Ir t //²+(4)² = f —1 +i ~L I =₍/²[_L_ +-L— | = d' ■ -r~ «;!“*1    23"‘ <Q:I siiiją _ _rfź ._ I+sin~ a

’ ^cos n>    l -sina) k cos* ar 2sin*«J    2sin² acos*’a    2sin⁷acos²«    2sin’acns²a

h -    ^ *^Mn ^ ■ Obliczamy pole powierzchni bocznej Ostrosłupa: /V 4 • -j-n/r = 2 •    V^{1 < s}-'"    = 2d~ ^słn *^<y

Jillnacma    ^J    1    2    sina ^ sintteoser    si»²acma'

stąd

488.

■W'

3ig?(Mg*f)

Rozwiązanie. Oznaczenia: a - długość krawędzi podstawy ostrosłupa.

a

W trójkącie //ATłV:    = stąd /; - — “ _a . W trójkącie SA'Ił': /r H²+(rę)². stąd

Jl-ig² §

// = «-*---.

Korzystając ze wzorów na pole trójkąta 5A'H' mo/emy zapisać równość:

.t    "    «

- ~-łę//. czyli - ^a -d =u~ ----. Stąd a = .    Zatem    . Objętość ostrosłupa: V=—a²H =-—-

“ •    ^2,t’:    ^4,S-    Jl-lg²"    ³ 3tg*(l-lg²f)

••OJ---j

M„²-lr^2b^: ,i²

Wskazówka. Korzystając 7. jiodobicństwa trójkątów /\VłV i .SWoraz AWW i 5f lf wyznacz h i X. Do wyznaczenia krawędzi podstawy < oraz. wysokości II ostrosłupa wykorzystaj mc. l'iio(;i>r,i.ui (patrz rysunek obok).

490.

1’ole: n~ -JJ . Objętość:

-V1

12

491. ^2.

Rozwiązanie. Należy obliczyć długość odcinka DE.

Punkt /> jest środkiem odcinka BC. więc l/l/Jł =■- - I. Punkt E jest śnxlkicm odcinka AS, więc odcinek ///. jest wysokością trójkąta równobocznego ABS. Wobec tego \BE\    Długość odcinka DE obliczamy korzystając / nr. /'itanortisa:

\PD^: = \BE\^: - IUD\^: = 3 - I = 2. stąd Il)E\ = Jl.

492. 60.

Rozwiązanie. Oznaczmy: a - długość krawędzi podstawy ostrosłupa. Należy znaleźć rr. Wiemy. >c: \KS\ = a. Punkt A'jest punktem przecięcia wysokości trójkąta równobocznego ABC. Zatem A'dzieli wysokość AD na ixlcinki będące w stosunku 2 : I. tzn.

lAAI = -=-l AD\.    więc 14 Al = -^.

^,gw"i^⁼^⁼rvT⁼^- ^więca"^w)>-