53 (225)

183

ODPOWIEDZI. WSKAZÓWKI. ROZWIĄZANIA

449.    Parabola o równaniu y--j^a*+.» ł 2.

450.    Zbiór A jest sumą dwóch prostych o równaniach y = 0 i y- tfi = 0.    451. Parabola o równaniu .v*-6> -3 = 0.

452. {u, V): (y = -y.r +■ I v y- [• «’ • l> a xe (-2; 2) a yt Rj.

Wskazówka. Jeśli punkt (y) jest środkiem okręgu <> stycznego wewnętrznie do okięgu o równaniu a' + ,v* = 4 i stycznego do prostej o równaniu y = 0. to promień okręgu o ma długość |y |. odległość punktu styczności okręgu o z. osią OYod punktu <0. 0) jest równa |«|. a odległość środka okręgu o od punktu (0. U) jest równa 2- |y].

453.    Parabola o równaniu y =    --ę.

454.    Parabola o równaniu y = 2r.

Wskazówki. Jeśli prosta przechodzi przez punkt <0.0), to jej równanie ma postać v=ru.

Jeśli punkty %,) i y.) są końcami cięciwy paraboli o równaniu y = x li nalcZą do prostej y-m. to odcięte tych punktów s.i to/.wiąza-

...    -t. + r,

nianii równania r - I =at. a odcięta środka cięciwy jest nwvna —^—•

455. u-5)^: + (y+21*= I.    456. 4n + fyfi.    457. 2ff-4.

458. 0=(3-,3—).    459. (.v + 4)*+ fy + 2)² = 36.    460. k = I lubk = -I.

STEREOMETRIA

463. fi dm\

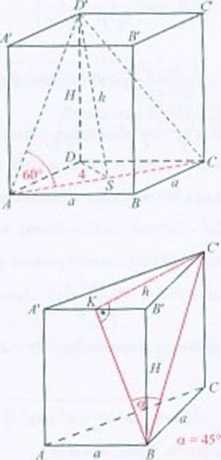
461. a) 112:    b)    462. ifitl¹ smacnsa | = fid²sin2« |.

464. lń/2.

Rozwiązanie.

Korzystając ze wzoru na długość przekątnej kwadratu, obliczam} długość krawędzi pinlsta-wy graniastoslupa: a fi - 4. stad o - 2/i. Trójkąt ACD' jest równoboczny, ponieważ kąty przy podstawie AC mają równe miar)’ wynoszące 60°. Zatem I AC = I Al/ I = | CD'= 4. Obliczamy długość wysokości graniastoslupa korzystając z nr. /'itagortisn (trójkąt CDI.Y)

H*«4⁷-afi)² =8. stąd II = 2/2.

Objętość graniastoslupa: V' = u * U ~ (2fi l ’ 2 fi = 16/2 •

465. 1000/6 cm¹.

Rozwiązanie

Obliczamy wysokość podstawy graniastoslupa: h    ₌ \ofi_m

Zauważmy, ze trójkąt BCK jest równoramienny, ponieważ, kąty przy podstawie HC mają równe miary (l/Ori = 45® i IZHCA1 = 1X0° -'Kr - 4S^# = 45"). Zatem Ifl/fl =10V?. Bok Utrójkąta UH 'K jest wysokością graniastoslupa. Obliczamy wysokość graniastoslupa korzystając z m. Pitagorasa (trójkąta 1111 'KY. H~ = 110/3)~ -Ul' 200. stąd // M>V2.

Objętość graniastoslupa: V'= ~—~ H = —• \ofi = 1000fi.

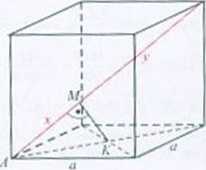
_<67.    , M_a.

Rozwiązanie. Należy obliczyć x = L-U/l oraz y = LWftl. Długość przekątnej sześcianu o krawędzi a jest równa o fi. 14181 = « fi. \AO = afi. LU1 = -~Trójkąt AKM jest podobny do trójkąta

„_iK Ml = gg. z*™ -fc = zjfe. «#