7 (1159)

ODPOWIEDZI. WSKAZÓWKI, ROZWIĄZANIA

137

2.22 53“ i 12T.

Rozwiązanie. ot - miara kąta ostrego równoległoboku. a+74* - miara kąta rozwartego.

Sanu miar dwóch kolejnych kątów równoległoboku wynosi 180°. zatem n + « + 74'¹ = 180°. Stąd a- 53°, « + 74°- 127'.

2.23 50\

fRozwiązanie. W czworokącie KBiJ) 90°+a+90° + 50¹ = 360^J. stąd «= 130’. (t+P= 180*, więc (I = 50“.

/	50	•/ fi.
/o	•i_	q/
		H

2.24 \ZA\=36®. IZ0I=45°. IZCI=I35°. IZ/)I=144\

WłkAzowka. Suma miar kątów pr/ylcgł>ch do ramienia trapezu wynosi 1X0°.

2.26 9.

Rozwiązanie, a. b - długości podstaw. « + fo+4 + 8 = 30. więc «+ />= IX. Długość d odcinka łączącego śtodki ramion trapezu jest równa połowie sumy długości podstaw, zatem </=9.

| Wskaż.

2.27 I lub 7.

:ówka. l*row.ul/ąc promienie do końców cięciw, otrzymamy trójkąty równoramienne.

2.28 R=3.

Rozwiązanie. Punkty A. B. C są wierzchołkami trójkąta prostokątnego, w którym 1401=3. l0Cl=0 + 2 i 140 = 0+1. Korzy stając 7. Iw. Pilago-ruta,otrzymujemy równanie <0 + 1 )*+3*=(0+2)\ Rozwiązaniem tego równania jest liczba 0 = 3.

2.29 8.

Rozwiązanie. Ok tęgi o środkach A i fi są styczne zewnętrznie, więc 1401=r+fi. Okręgi o środkach 4 i 0są styczne wewnętrznie do okręgu o( C. 41. więc Hfl=4-r i 100=4-0. Obwód trójkąta ABC: r+R + 4-r+4-0 = 8.

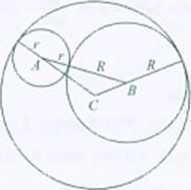
230 140".

ązanie. a- miara kąta między stycznymi. Oba promienie i poprowadzone styczne wyznaczają czworokąt. Styczna tworzy / promieniem, przez którego koniec została poprowadzona, kąt prosty. Zatem wyznaczony czworokąt ma kąty o miarach 90°. ‘/O⁵. 41) . a. Suma miar kątów ) czworokąta jest równa 36(1°, zatem 90' + 90“ + 40° + a = 360°. Stąd otrzymujemy a = 140°.

2.31 i j 12.

5    5

Rozwiązanie. Z podobieństwa trójkątów WAP i WRS mamy    stąd 0—1.5r.

ra = nra-HV/*l = 4 = r+R s r+ 1,5r = 2.5r. lnem i = l,6. zaś 0=2.4.

2.32 l/’t)l: 1S01 = I: J5.

óązanic. Z Zn . o związkach miarowych między odcinkami stycznej i siecznej mamy >.W. Stąd h=afl. Zatem \PQ\: LS0I = I: fi.

233 li2.

Rnrwtąianio. Podstawa trójkąta ma długość 3. i + y = 3. a z nr. o związkach manny h między odcinkami stycznej i siecznej mamy «< \ +y)= 1^3)*. Zatfmrnl.zaś v=2.

LZ.