52 (212)

182 ODPOWIEDZI, WSKAZÓWKI. ROZWIĄZANIA

433. C' -(-3. -7). />-<9. 5>. Pole trapezu: 30.

Rozwiązanie. Niech C=(.v<-. v, ) i « = (**>-,.1.    KIJ -2- BA. KD = (.v„-3.y*+ l|, 2 BA = 2|3, 3)-16.6J, żalem *„-3 = 6 i y„-M=6.

Stąd *„=9 i y_n=5. Punkt A'jest środkiem odcinka CD. więc 3=0,5(.\_l/+9) i -I =0,5(»+5). Sląd r<=-3 i »-=-7.

Pole trapezu P 0,5 (! AU i + 4-1 AU [ \h - 2.5/j ' AU I.    I AU I = 3 VI, wysokość h jest równa odległości punktu K od prostej AU. która ma

równanie.v-y=0, więc h = -—L * - -L = 2v2. Zatem P=2.5 • 3-Jl 2-fi = ,3l). v2 V2

434.    Odcinek KI. nie ma punktów wspólnych z. daną prostą.

435.    n> Ohs/ar między prostymi y = 0.5.i i y-0.5.v — 2:    bj płaszczyzna:    c) ta półpłaszcz.yzna (bez brzegu i wyznaczona pr/cz prostą

y=l).5v-2. <ło której nałczy punkt (0. -3).

436.    a) Rys. I/3M; b) 5.

437.    b) |_2    < 3'^:    c) punkt /‘=(2-^; - nic należy do czworokąta (rzędna tego punktu jest mniejsza od-2).

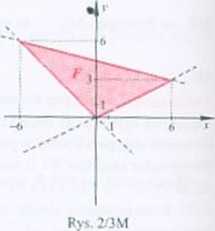
438.    Rys. 2/3M: pole figury F: 27.

[*4420

439.    a) a-2yS0 .    b)h=-\A.

| v-y-r5e0

yS*-2

440.    a)/l = (2^:4). /f=<8.6>:    b) vi-* + 3    .

v < -OJ* 4- KI

441. Trapez o wierzchołkach (-2, 0). (2.0). (2, 4.5 j. <-2. I.5i Pole trapezu: I2.

442. Zbiór A: pas. którego brzeg tworzą proste y = 1\ - 2 i y - 2\ - 4: zbiór U: dwie rozłączne pólpłaszc/.Yzny (bez brzegu t wyznaczone pi/c.r P>ostc y = -3v + 2 i v = 3*-2: zbiór A nil': równolcgłobok o bokach zawartych w podanych wcześniej prostych.

Wskazówka. |y-2i t-3|<l « <y-2v+3>-1 av-2v+3SI).    |y+3x|>2 » <v+3v<-2 v v+3*>2>.

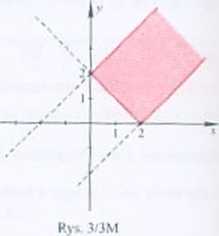
443.    Rys. 3/3M.

444.    a) rozwiązaniem układu nierówności jest każda para liczb postaci (-o + b - I. 2o - b f 2).

gdzie a G R.iieR,:    b) rozwiązaniem układu nierówności jest każda para liczb postaci

_gJ/ich€ u..

445.    i = -1. y = 2 lub x = I. y = I) lub * = 3. y = 2.

446.    .v = -3. y = 2 lub .r - -2. y - 3 lub x = 2. y = -3 lub .« = 3. y - —2

(równanie Id + lył 5 opisuje brzeg kwadratu o wierzchołkach (5. (I). <0. 5), i 5. Ol. (0. -5.) I.

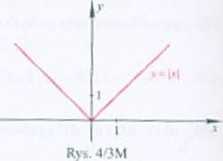
447.    Rys. 4/3M.

448.    o = -1 lub a = 3.

Rozwiązanie. Nierówność r + y+2* -I I sprowadzamy do postaci (r f I)^: ł-y’<2. Nierówność ta opisuje kolo o środku w punkcie 5- (-1.0) i promieniu o długości *'2. Równanie x-y t-./ = l> dla każdej wartości parametru o jest równaniem prostej. Dany układ ma dokładnie jedno rozwiązanie wtedy i tylko wtedy, gdy prosta o równaniu x -y -t a =0 jest styczna do kola US. V2).

czyli gdy odległość .7 punktu S od danej prostej jest tówna _v'-. d = ——• = ,2.

VI VI

Stąd « = -l lub o=3.