1

Rachunek nuwnoPoooBiEśWA / statystyka matematyczsa - INF MD

I TestB	ZaKJIŁ-ŚLIĆ ZWK1EM X JEDNĄ ODPOWIEDŹ
1 Z.ADA.ME	Odpowiedz
I ]	A	! B	C I D
2	A	1 B	C	D
3	A	B	! c	i o
1 ^1	A	I B	i ^c	D
5	A	B	c	D
6	A	B	c	D
I 7	A	1 B	c j	D
8	A	B	C	D
^9	A	B	c	D
^10	A	3	c	D
I ^11	A	B	c	D
12	A	B	C i	D
^13	A |	B	c j	D
1 ^14	a i	B i	c	D
^15	A i	B	c 1	D
^16	A !	B	c	D
17	A ]	B j	c ^:	D
18	^A 1	B	C i	D
19	A i	B	C j D
^20	A	B	C ; D
^21	A	B	c ,	D
^22	A	B	c	D
^23	A	B	c	D
I 24	A	B	c	D
f 25	A	B	c	D
I 26	A	B	c	D
1 27	A	B	c	D
1 ^28	A	B	c	D
^29	A	B	c	D
I ^30	A	B	c	D
I ^31	A	B	c	f D
32	A	B	C	^D
33	A	B	^c	D I
34	A	^B	c	D 1
35	A	B	c	D 1
36	A	B	c	D I
37	% A	B	c	loi

Imię i nazwisko

GRl Tk

1. Wzrost (w cm) chłopców u wieku 9 lat jest zmienną losową o rozkładzie normalnym A/(135.10). Prawdopodobieństwo, że zmienna ta przyjmuje wartości różniące się od średniej o me mniej ntz 4 cm wynosi:

C. 0,6554; D 0.3108.

A.    0.6892;

B.    0,3446;

2.    Każdy podzbiór zbioru zdarzeń elementarnych Cl jest zdarzeniem losowym, gdy-

A.    przestrzeń Cl zdarzeń elementarnych jest zbiorem skończonym

B.    przestrzeń Q zdarzeń elementarnych jest zbiorem przeliczalnym:

C.    przestrzeń Cl zdarzeń elementarnych jest zbiorem nieprzeliczalnym;

D.    zawsze tak jest

3.    Obsługa działa arty leryjskiego ma 3 pociski. Prawdopodobieństwo trafienia do celu jednym pociskiem (przy 1 wystrzale) wynosi 0,7. Strzelanie kończy się z chwilą trafienia do celu albo wyczerpania pocisków. Prawdopodobieństwo oddania co najmniej 2 strzałów jest równe:

A.    0,3;

B.    0,30,7; ^{1 2}

C.    0.3²;

D.    0,3² -0.7.

A.    niemierzalną;

B.    typu ciągłego;

C.    typu skokowego;

D.    inną.

6. Wektor losowy (A, Y) jest typu ciągłego o gęstości danej wzorem:

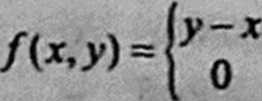
dla xe(0,l)AyG(l,2) dla. xe(0,l)v^6(1,2)’

A.    niezależne;

B.    zależne;

Zmienne A i Y są:

C.    meskorelowanc;

D.    typu skokowego.

Opracowała Joanna Banaś

1

   Nierówność Rao-Cramera jest wykorzystywana do dowodzenia, że:

A.    estymator jest zgodny;

B.    estymator jest nieobciążony;

C.    estymator jest najefektywniejszy;

D.    estymator jest obciążony.

2

   Badając zbiorowość studentów w Polsce ze względu na częstość korzystania z bibliotek (często, rzadko itp.) mamy do czynienia z cechą: