15

w terenie dowolny punkt luku P i styczną do niego w tym punkcie.

Jeżeli poczynając od tego punktu odłożymy na łuku równe odcinki PI, 12, 2 3,..., a następnie połączymy punkt P cięciwą z każdym z otrzymanych punktów pozostałych, to cięciwy te utworzą między sobą jednakowe kąty obwodowe cp, równe połowie odpowiadającego im kąta środkowego 2cp, wspierają się one bowiem na równych sobie łukach (rys. 41). Kąt, jaki ze styczną w punkcie P tworzy najbliższa cięciwa PI, jest także równy cp, co wynika ze znanego z geometrii twierdzenia o kącie między styczną i cięciwą.

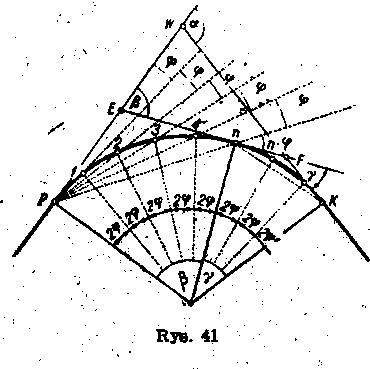
Chcąc wytyczyć równe i okrągłe odcinki łuku AL, wy^teiące nip. 10 lub 20 m, obliczamy kąt środkowy 2cp, jaki odpowj||j| temu odcinkowi. Otrzymamy go z wzoru    ₄    . i

„ AL    AL    W*'    /'

² ? =    ł ⁼ -2R'^e    (S1

lub odczytamy z tablic do tyczenia krzywych. Długość AL obie ramy taką, aby dla danego promienia można było przyjąć ją jak równą cięciwie, lub też obliczamy cięciwę dla danego odcink łuku AL ze znanego już wzoru

c = 2’jR sin cp.

Tyczenie możemy wykonać w ten sposób, że na punkcie ustawiamy teodolit i od stycznej odkładamy kąt cp. Na wyznaczonym kierunku odmierzamy cięciwę PI = c, odpowiadającą przyjętemu odcinkowi łuku. W ten sposób otrzymujemy punkt 1. Następnie odkładamy od stycznej kąt 2<p i do wyznaczonego już punktu 1 przykładamy początek taśmy, po czym długością obranej cięciwy zataczamy taśmą łuk dotąd, aż obraz szpilki, przyłożonej do odpowiedniego odczytu na taśmie, znajdzie się na nitce pionowej teodolitu. W ten sposób otrzymujemy punkt 2. Podobnie tyczymy następne punkty 3, 4,... , n odkładając kąty 3cp 4((,... , nq) i szukając przecięcia otrzymanego kierunku z cięciwą odmierzoną od punktu ostatnio wytyczonego.

Jeżeli przeszkody terenowe uniemożliwiają dalsze celowanie, to teodolit przenosimy na wyznaczony już n-ty punkt, w którym styczna tworzy z przedłużeniem cięciwy Pn kąt równy n • q>. Stycznej w tym punkcie nie musimy jednak w terenie wytyczać, gdyż zamiast odkładać od niej kąty cp, 2cp, 3<p możemy odkładać od wyznaczonej już cięciwy nP kąty:    '    ,,

(i80°—n<p)~ <p (180°—n<p)—2<p ;

Tycząc okrągłe odcinki łuku (np. 10 lub 20 m), otrzymamy zwykle po dojściu do punktu końęjcwtego peymą resztę AL', dla której kąt obwodowy <j>'_ i pdpbwłędttią cięciwę obliczymy podobnie jak poprzednio dla łuku AL*’/ _t ; /

Punkt hektometrowy 'wyznaczymy najłatwiej obliczając kąt obwodowy dla różnicy łuku .między punktem hektometrowym a najbliższym wyznaczonym już punktem b okrągłej długości łuku. Jeżeli na przykład punkt heKtometrpwy llf ^najdzie się między punktami 3 i 4, to kąt obwodowy i cięcróę obliczamy dla łuku 3M lub M4.    '    ■

Najkorzystniej jest obierać na łuku jedno stanowisko w po

|n dwóch gałęzi łuku na-)żenie punktu n w tere-JWy, a więc i kąt zwrotu

bliżu jego środka, np. na punkcie n (rys. 41), a tyczenie wykonywać nie w przód, lecz wstecz (na siebie), poczynając od punktów położonych najdalej od teodolitu (punkty P i K na rys. 41). Ten sposób tyczenia jest dokładniejszy, błędy bowiem w pewnym topniu kompensują się. Wprawdzie błąd odkładania długości rzrasta, lecz wpływ błędu kierunku |

Do wytyczenia z jednego stanowią leży przedtem wyznaczyć dokładnie | nie. Zgodnie z rysunkiem 41 kąt śrc

stycznych dla n-tego punktu, wyniesie (J = 2ncp, a dla reszty łuku y ~ <x —p. Dla kątów p i y znajdziemy z wzoru (16) długości stycznych PE = En oraz nF = FK. Mając te wielkości możemy położenie punktu n wyznaczyć jedynie na podstawie pomiarów liniowych.

Łuk kołowy można również wytyczyć metodą biegunową dzieląc go na określoną liczbę m równych, chociaż zwykle nie-okrągłych części. Jeżeli dla całego łuku kąt środkowy jest równy a, to dla obranego odcinka łuku kąt środkowy wynosi 2<p = —

7Tt

79

%