4 (374)

AtBg [s]		mu
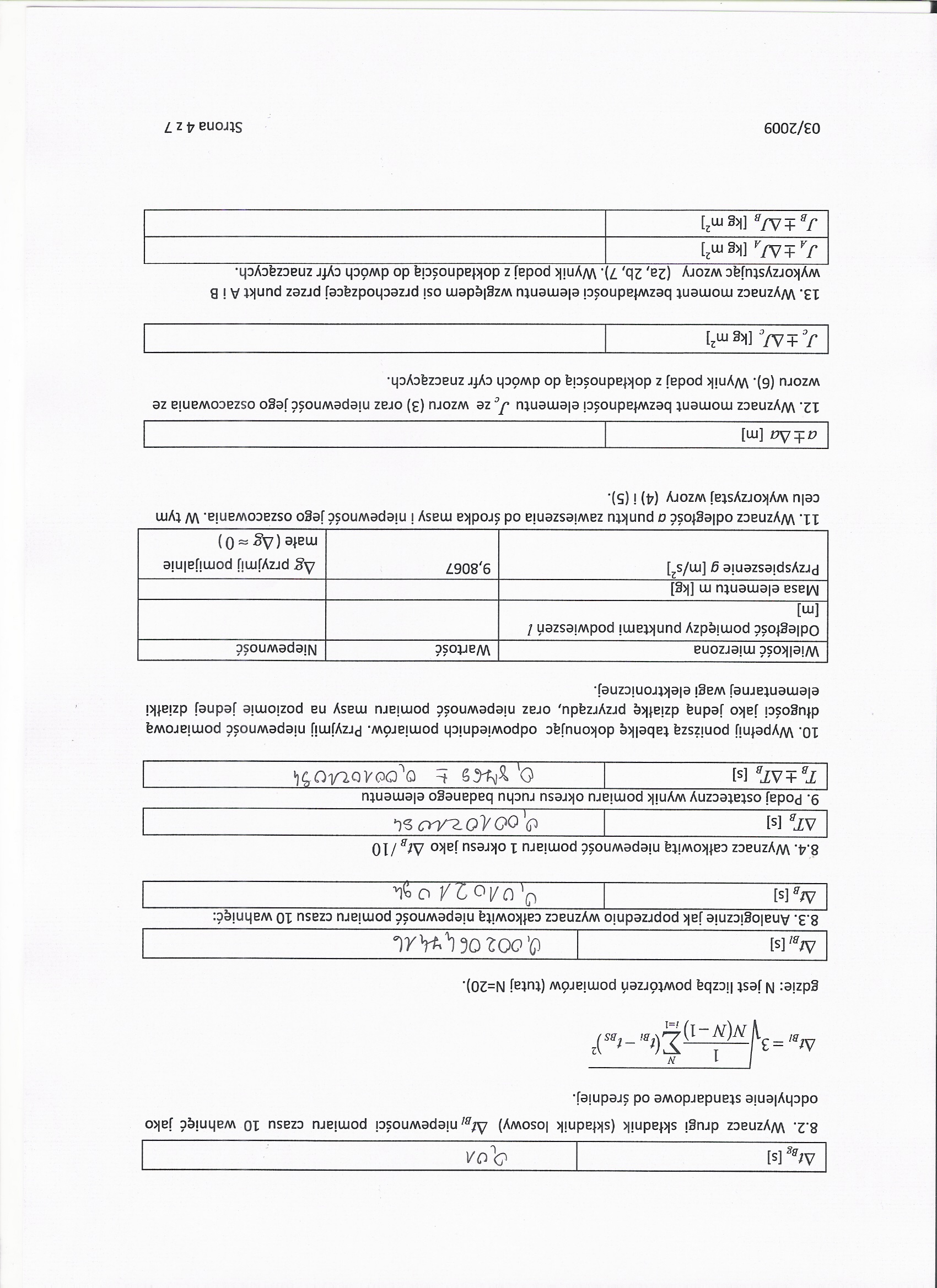
8.2. Wyznacz drugi składnik (składnik losowy) AtBl niepewności pomiaru czasu 10 wahnięć jako odchylenie standardowe od średniej.
1 1 ^N / ^Al- ^3]In(n-i)S^‘ ^hs	f
gdzie: N jest liczbą powtórzeń pomiarów (tutaj N=20).
WBBk		C9,002 0£ ^AL
8.3. Analogicznie jak poprzednio wyznacz całkowitą niepewność pomiaru czasu 10 wahnięć:
A^[s]
Ś.4. Wyznacz całkowitą niepewność pomiaru 1 okresu jako AtB /10
ATb [s]	0{ OOĄ.O'ŁJUJ SU
9. Podaj ostateczny wynik pomiaru okresu ruchu badanego elementu
Tb±ATb [s]	O, t o^ooa.ozAo^

10. Wypełnij poniższą tabelkę dokonując odpowiednich pomiarów. Przyjmij niepewność pomiarową długości jako jedną działkę przyrządu, oraz niepewność pomiaru masy na poziomie jednej działki elementarnej wagi elektronicznej.

Wielkość mierzona	Wartość	Niepewność
Odległość pomiędzy punktami podwieszeń / [m]
Masa elementu m [kg]
Przyspieszenie g [m/s^2]	9,8067	Ag przyjmij pomijalnie małe (Ąg«0)

11. Wyznacz odległość a punktu zawieszenia od środka masy i niepewność jego oszacowania. W tym celu wykorzystaj wzory (4) i (5).

a±Aa [m]
12. Wyznacz moment bezwładności elementu Jc ze wzoru (3) oraz niepewność jego oszacowania ze wzoru (6). Wynik podaj z dokładnością do dwóch cyfr znaczących.
[kg m^2]

13. Wyznacz moment bezwładności elementu względem osi przechodzącej przez punkt A i B

Ja±AJa [kgm^2]
Jb±AJb [kg m^2]

03/2009

Strona 4 z 7