matmadodomu

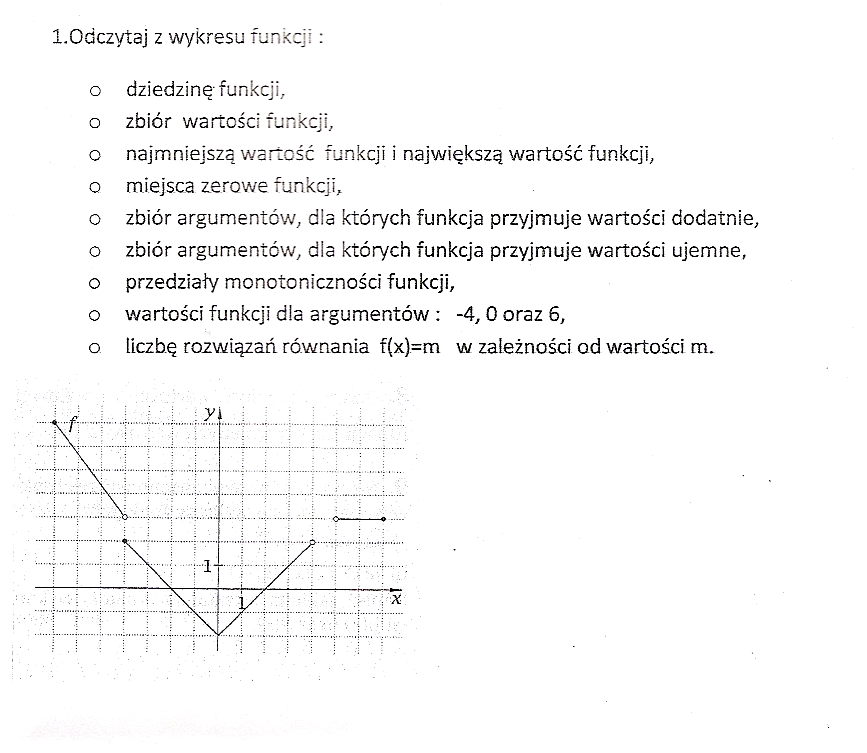
1.Odczytaj z wykresu funkcji:

o dziedzinę funkcji, o zbiór wartości funkcji,

o najmniejszą wartość funkcji i największą wartość funkcji, o miejsca zerowe funkcji,

o zbiór argumentów, dla których funkcja przyjmuje wartości dodatnie, o zbiór argumentów, dla których funkcja przyjmuje wartości ujemne, o przedziały monotoniczności funkcji, o wartości funkcji dla argumentów : -4,0 oraz 6, o liczbę rozwiązań równania f(x)=m w zależności od wartości m.

; f ..............y
	.......I.......f.......j.....i.....j—.............
] i .!
- y	• t