FizykaII48701

483

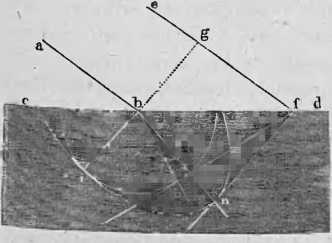
Wiedząc to, przez uogólnienie wyżej (§ 74) podanego wykreślenia, nie trudno do każdego, w jakimkolwiek kierunku na spat islandzki padającego promienia światła wynaleść kierunek obu w nim załamanych promieni, zwyczajnego i nadzwyczajnego- Z punktu padania światła jako punktu środkowego, opisu-J^e się najprzód kulę promieniem dowolnej wielkości r. potem ^elipsoidę powstałą przez obrót elipsy, mającej większą oś a, mniejszą /;, około tejże osi mniejszej, leżącej w kierunku osi spatu, uwzględniając przy tern proporcyą r: a : b = 1: OG742 :0‘6045, ^a nareszcie znowu kulę, która dotyka się elipsoidy w punktach końcowych osi obrotu. Zrobiwszy to, przedłuża się kierunek Promienia padającego aż do powierzchni kuli pierwszej i wy- » stawiwszy do niej w tym punkcie jej przebicia płaszczyznę sty-czną, wynajduje linię przecięcia się tej płaszczyzny z płaską ścianą spatu, na którą pada światło. Przez tę linię kładzie się jedne płaszczyznę styczną do elipsoidy, drugą do kuli w niej zatoczonej i od punktu padania światła prowadzi do obu tych punktów stycznych linie proste. Ta z nich, która odpowiada Powierzchni kuli, wskazuje kierunek promienia zwyczajnie załamanego, która zaś należy do elipsoidy, daje kierunek promienia nadzwyczajnego. Podobnym sposobem można do każdego promienia załamanego wynaleść zawsze kierunek drugiego załamanego i promienia padającego, który przy załama-mu na te dwa rozpada się, tudzież kierunek promienia, występującego ze spatu w powietrze W razie przeto, gdy optycz-ua oś kryształu na płaszczyźnie padania promienia światła ab (Fig. 264), zatem w naszym rysunku na płaszczyźnie papieru

big. 264.

leży i ma kierunek bi, prowadzi się do linii ab równoodległą ef, tudzież z punktu padania b na linii cci, powstałej z przecięcia górnej ściany kryształu z poziomą płaszczyzną, linię prostopadłą bg do ef, opisując około ,tego punktu b koło, którego