0100

§ 2. Granica funkcji

101

Zamieniając tu x na x* (śr>0), łatwo dowieść, że również

log.*

lim

x-+ + oo X"

- =0 (o>l, k>0).

Rzeczywiście, jeżeli dla dowolnego e>0, obrać A tak, żeby dla x>A spełniona była nierówność

log.*

■<ke,

to dla x>Ai = A^llk będzie x*>A oraz

iog„x

■ <e.

Jeżeli teraz x zastąpimy przez 1/*, to otrzymany wynik przybiera postać

lim jc*log.*=0 (a>l, k>0).

*-*+o

6) Z udowodnionego w ustępie 25, 5) związku

lim a^1/n=l,

można otrzymać związek ogólniejszy Zauważmy, że oczywiście również

lim a =1 . *-.0

1

lim a~^1,n— lim -^=1.

n-» + co    n~* + cod

Dlatego dla dowolnego e>0 można znaleźć taki wskaźnik n₀, że (dla a>l) l-e<a'^i,"⁰<a^,"°<l+s.

Jeżeli teraz

\x\<\jn₀, czyli    — l/n₀<*<l/n₀,

to

skąd

a~^u*< a^x<a^u*°

1— e<a*<l+e, czyli    la¹ — 11 <e,

co dowodzi wskazanego twierdzenia.

7) Teraz ustalimy następujący związek, ważny w dalszym ciągu:

(8)

sin*

hm ——=1.

*~o x

Przede wszystkim jednak udowodnimy pewne pożyteczne nierówności:

(9)    sinx<x<tgx (O-occ^n).

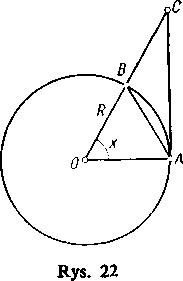
W tym celu w kole o promieniu R rozważmy kąt ostry AOB, cięciwę AB i styczną AC do okręgu w punkcie A (rys. 22). Mamy wówczas:

pole A zł OB < pole wycinka AOB< pole A AOCi¹).

O Posługujemy się przy tym tymi własnościami pól figur elementarnych, które znane są ze szkoły średniej.