0164

166

X. Zastosowania rachunku całkowego

Do przedziału </₀, Ty i do pokrywającego go układu otoczeń 2" = {a} zastosujemy teraz lemat Borela [88]; cały ten przedział można zatem pokryć skończoną liczbą takich otoczeń, a więc krzywa rozpada się na skończoną liczbę łuków, z których każdy daje się wyrazić równaniem postaci (5) (jednego lub drugiego typu). Wystarczy teraz powołać się na wynik udowodniony wyżej. Tak więc:

Jeśli figura Pjest ograniczona jedną lub kilkoma krzywymi gładkimi, to jest ona mierzalna.

Wynik ten zachowuje moc również w przypadku, kiedy krzywa ma skończoną liczbę punktów osobliwych, oddzielając bowiem te punkty za pomocą otoczeń o dowolnie małym polu będziemy już mieć do czynienia z krzywymi gładkimi.

338. Wyrażenie pola za pomocą całki. Przechodzimy teraz do obliczania pola za pomocą całki.

Przede wszystkim rozpatrzymy — po raz pierwszy w sposób ścisły — znane nam już zadanie znajdowania pola trapezu krzywoliniowego ABCD (rys. 18). Figura ta jest ograniczona z góry krzywą DC, która ma równanie

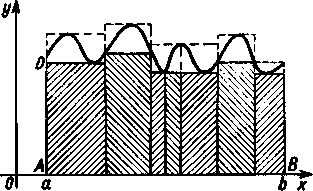
Rys. 18

y=m,

gdzie f(x) jest funkcją dodatnią i ciągłą w przedziale (a, bj. Z boków trapez ten jest ograniczony odcinkami pionowymi AD i BC (każdy z tych odcinków może się redukować do jednego punktu), a z dołu odcinkiem AB osi x. Istnienie pola \P\ rozpatrywanej figury ABCD wynika właściwie z twierdzeń udowodnionych w poprzednim ustępie i chodzi tylko o obliczenie tego pola.

W tym celu przedział (.a, by rozbijamy, jak zwykle, na podprzedziały wstawiając między a i b punkty

a — x₀ <    < x₂ < ... < x₍ < x₍₊₁ < ... < x„ = b.

Oznaczmy przez m, i Af, odpowiednio wartość najmniejszą i największą funkcji f(x) w i-tym przedziale (x,, x,₊₁> (i = 0, 1,... ,n — l), a następnie utwórzmy sumy Darboux

s = ^ m_t Ax_t, S=^M, Ax_t.

i    t

Wyrażają one oczywiście pola figur schodkowych utworzonych z prostokątów odpowiednio leżących pod krzywą i wychodzących ponad nią (patrz rysunek 18). Dlatego mamy

s<\P\<S.

b

Jeśli największa z różnic Ax, dąży do zera, to granicami obu tych sum jest całka J/(x) dx (¹),

(') W myśl 336, 1) dowodzi to już mierzalności trapezu krzywoliniowego ABCD; aby otrzymać wzmiankowane tam ciągi figur, można na przykład dzielić przedział na równe części.