0185

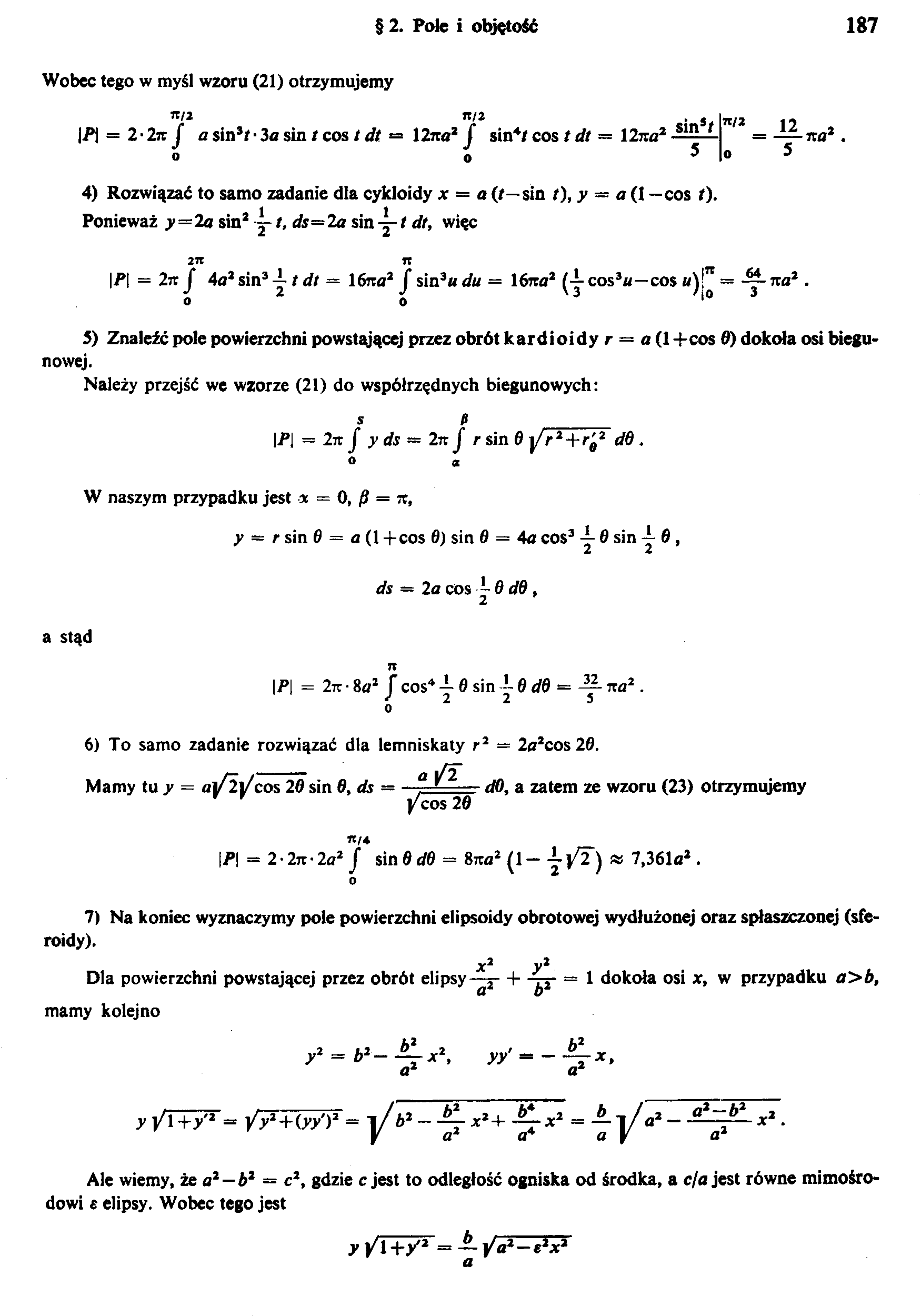
187

§ 2. Pole i objętość

Wobec tego w myśl wzoru (21) otrzymujemy

nn

|.Pj = 2 • 2jt j a sin³/ ■ 3a sin / cos t dt — 12jt«³ j sin⁴/ cos t dt = 12iza²

sin⁵/

^71,2 = i!

o 5

4) Rozwiązać to samo zadanie dla cykloidy x = a (/—sin /), y — a (1 — cos /). Ponieważ y=2a sin² ~ ^t< ds=2a sin-j-t dt, więc

27*    Tt

|P| = 2n J 4o² sin³ y / dt = 16rca² J sin³« du = I6na² (y cos³«—cos = -y- na² .

5) Znaleźć pole powierzchni powstąjącej przez obrót kardioidy r = a (1 +cos 0) dokoła osi biegunowej.

Należy przejść we wzorze (21) do współrzędnych biegunowych:

s    »

\P\ = 2n j y ds = 2n j r sin 0 \/r²+rg² dO .

o    a

W naszym przypadku jest x = 0, /? = Tt,

y — r sin 0 = a (1 +cos 0) sin 0 = 4a cos³ y 8 sin y 0 ,

ds — 2a cos y 0 dd ,

a stąd

Tt

|P| = 2k • 8a² J cos⁴ y 0 sin — 0 d8 — -y- na² . o

6)    To samo zadanie rozwiązać dla lemniskaty r² = 2o²cos 20.

Mamy tu y = ul/2l/cos 20 sin 0, ds = ■ f dO, a zatem ze wzoru (23) otrzymujemy ^{r r}    cos 20

IPI = 2-2n-2a² f sin 0 d8 = 87ta² (1 - -i-yT) » 7,361a² .

O

7)    Na koniec wyznaczymy pole powierzchni elipsoidy obrotowej wydłużonej oraz spłaszczonej (steroidy).

Dla powierzchni powstającej przez obrót elipsy yj- + yj- = 1 dokoła osi x, w przypadku a>b, mamy kolejno

y² = b¹---x², yy =---x,

a²    a²

y /T+7^r=    1A² - -4 **+ -*r X² = - |/fl* - X² •

y    a²    a*    a \    a²

Ale wiemy, że a¹—b² = c², gdzie c jest to odległość ogniska od środka, a c/ajest równe mimośro-dowi e elipsy. Wobec tego jest

y V1 +/² = — ^a²—e²x² a