280 (19)

560 21. Synteza dwójników pasywnych

Mamy dalej

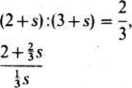
wobec tego

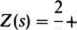
(21.34)

s 2 js s 3 ⁺ 3+l

s

2 1 -+-

skąd wynika połączenie Cauera z rys. 21.22.

Gdy podczas dzielenia wielomianów otrzymuje się współczynniki ujemne, wówczas należy zmienić sposób postępowania. Można zastosować drugi sposób dzielenia, na przykład zamiast rozpoczynać dzielenie od najwyższych potęg, należy rozpocząć dzielenie od najniższych potęg. W ten sposób można często otrzymać ułamek łańcuchowy o dodatnich współczynnikach, a jego realizacją jest połączenie Cauera. Gdy metoda rozkładu na ułamek łańcuchowy nie prowadzi do celu, należy zastosować inną metodę.

Przykład 4. [6] Wyznaczymy schemat dwójnika o impedancji

2sⁱ + 3s² + 2s + 1

Rozpoczynając dzielenie od najwyższych potęg, mamy

s² + s + 1

Dzieląc wielomian 2s² + 2s+l przez s²+s+l, otrzymuje się współczynnik ujemny. Wobec tego rozpoczynamy dzielenie od najniższych potęg

(1 + 2s + 2s²):(l +s + s²) = 1,

1 + s +s^:

a więc

Z{s) = s+

1 +

= s +

1 +

1 +s + s²

S + S"

Otrzymujemy dalej

, 21.23. Realizacja impedancji wyrażonej wzorem (21.35)

K)^5,

wobec tego

(21.35)

Z(s) = sH----= s +

	1+—
1 s^2	1
+ ,	-+
s s^z + s	s

skąd wynika połączenie Cauera z rys. 21.23.