0018

20

VIII. Funkcja pierwotna (całka nieoznaczona)

Zauważmy, że zawsze, gdy całka ma postać

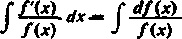
a więc gdy w wyrażeniu podcałkowym licznik' jest różniczką mianownika, podstawienie / = f(x) prowadzi do celu:

J-y--ln|/| + C = ln|/(*)| + C.

Zgodnie z powyższym mamy

[por. 4)(b)j;

(b)    f ctgxdx-=    = In |sin jr|+C,

J    J sin x

(c)    f - dx = — f^{d (e}**⁺    - — ln (e²*-|-1)+ C,

sin x cos x

6) Z ostatniej całki otrzymujemy łatwo dwie następujące pożyteczne całki:

(d)    f—^--f ***** = In Itg^i+c.

J sin x cos x J tg x

(a)

<b)

/

f—- f—¹

J S\nx J sin —

.dx

^{= ,n} *^gT ^x

+C,

(b)

sin (*+ ±k)

7) (a) I t^^arc *g ₍/a = f i/arc tg x darc tg x = 4(arc tg x)^3/2 + C, J l+x    ■/    3

=    --arctg^+C,

J e^2x+I J (e*)²+l

(c)

e^2x+l J (e*)²+l

f_tg±-4__ U-U-L-m

A¹ a:² J    x

cos —

X

+ C

[patrz. 4) (b)].

Podamy teraz kilka przykładów całkowania wyrażeń zawierających dwumiany kształtu a²—X¹, x²+ ■j-a² i x²—a². W tych przypadkach wygodnie bywa zwykle zastąpić x przez funkcję trygonometryczną lub hiperboliczną nowej zmiennej t i skorzystać z równości

sin²/+cos²/ = 1,    1+tg²/——

cos²/

cosh²/

cosh²/—sinh²/= 1,    1—tgh²/

⁸⁾/t?

dx

(x²+a²)² Podstawienie: x = a tg t (*), dx

a dt

, x²+a²

-, a więc

cos²/    cos²/

f ,    ~ ~T f cos¹'* = -rV(/+sin/cos/)+C.

J (x²+a²)² a³ J    la³

[267,(17) (a)].

(') Przy czym wystarczy założyć, że / zmienia się między — rc i -i- w.