0034

36

VIII. Funkcja pierwotna (całka nieoznaczona)

Tak więc szukana całka jest równa

/

4x⁴4-4x»-H6*²+12x+8 .

(*+i)^ł(jc²+n^ł    *

x² — x+4 *³+jr²+*+l

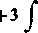
dx

x²+l

+3arctg*-t-C.

x²-x+4

JC³+JC²+JC+1

W przykładzie tym obliczenie ostatniej całki można było łatwo wykonać od razu. W innych przypadkach trzeba znowu rozkładać na ułamki proste. Można zresztą czynność tę połączyć z poprzednią.

277. Przykłady. Podamy dalsze przykłady całkowania funkcji wymiernych.

/dx

+jc^ł)^ł • ^{Rozldad na u,am}ki proste otrzymujemy tu poprzez nieskomplikowane przekształcenia

1    ₌ (1+S²)-*² ₌    1___I_ ₌ (1 +jX²) — x²___1_

jc²(1+*²)²    *²(1+*²)²    jc²(1+jc²)    (l+x²)²    x²(l+;c²)    (l+x²)²

₌ j___i___i_

X²    l+x²    (1+*²)² '

Odpowiedź: — ---^—--7-,— 4 ^arc tg *+ C.

x 2    1+jt^2    2

2) f-:

J (2x—

4x²+4x—l\

(2x-l)(2x+3)(2*-5)

dx.

Mamy

4x²+4x— II

±x²+±x-

U

B

(2jc— 1) (2jc+3) (2jc—5) skąd wynika tożsamość

*+ł

^x~\

ł*^J+ T*-T-^A (^x+ i)(^x~ i) +*(*- i)(*“ i) +^c(^x~ ł)(*+1) •

Zamiast przyrównywać współczynniki przy jednakowych potęgach x w obu stronach równości, można postąpić inaczej. Podstawmy w tej tożsamości kolejno x = -ł-. —j. -y • Otrzymujemy od razu A = —, B = —— , C = —, przy każdym bowiem podstawieniu z prawej strony pozostaje tylko jeden

4-    8    8

składnik.

(2x—l)^ł(2x—5)³ _+c.₍₁₎ 2x+3 I

Odpowiedź: jln |x- -i-j - 7^,n|*+ i|⁺ 7^ln|*~ f|^+C= i^ln

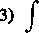
dx

x*+l ‘

Ponieważ

*⁴+l = (je⁴+2jr²4-l)—2jc² = (x²+l)²-(xj/'2)² = (x²+x^2+l)(x²-x/2+l), przeto szukamy rozkładu w postaci

1    ₌_Ax+B ₊ Cx+D

**+l    x²+x]/2+\ x²-*yT+l

Z tożsamości

I = (Ax+B){x²-x^2+\)+(Cx+D)(x²+xf2 +1)

C) Stała C' różni się oczywiście od stałej Co — | ln 2.