0038

40

VIII. Funkcja pierwotna (całka nieoznaczona)

wówczas

gdzie

t =

V

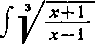
dx

*+l

-3 dt f²-l

= _Lln 2

x+l x-\ ■

/(

I

f-1

+

t+2    \

/²+t+i;

dt =

f² + f-i-1

0-D²

+ ]/$ aretg

2f—1

]/f

+ C,

279. Całkowanie różniczek dwumiennych. Przykłady. Różniczkami dwumiennymi nazywają się wyrażenia postaci

x^m(a + bxⁿY dx,

gdzie a, b> są stałe, a wykładniki m, n, p są liczbami wymiernymi. Wyjaśnimy, w jakich wypadkach wyrażenia te można scałkować w postaci skończonej.

Jeden z takich przypadków jest widoczny od razu: jeśli p jest liczbą całkowitą (dodatnią, zerem lub ujemną), to rozpatrywane wyrażenie należy do typu zbadanego w poprzednim ustępie. Jeśli oznaczymy mianowicie przez X najmniejszą wspólną wielokrotność mianowników ułamków m i n, to będziemy mieli do czynienia z wyrażeniem postaci

A /—    A t—

R (V x) dx, a więc dla sprowadzenia go do postaci wymiernej wystarczy podstawić t = \ x. Przekształćmy teraz dane wyrażenie za pomocą podstawienia z = x". Otrzymamy

1    -"ii -i

x^m(a + bx”)^p dx = — (a + bz)^p z " dz . n

Oznaczając krótko

m + 1    ,

mamy

(2)

/

x^m(a + bx”)^pdx

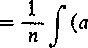
+ bz)^pz^ądz .

Jeśli q jest liczbą całkowitą, to otrzymamy znów wyrażenie zbadanego już typu. Rzeczywiście, jeśli oznaczymy mianownik ułamka p przez v, to wyrażenie przekształcone

^V /-

będzie miało postać R(z,ya+bz). Sprowadzenie do postaci wymiernej wyrażenia podcałkowego można też osiągnąć od razu przez podstawienie

t = ]/a + bz =^v^a + bx".

Przepiszmy wreszcie drugą z całek (2) tak:

a + bz

z^{P in}dz .

Łatwo dostrzec, że jeżeli p + q jest całkowite, to otrzymamy także przypadek zbadany:

wyrażenie przekształcone ma postać R

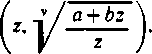
Wyrażenie

podcałkowe