0022

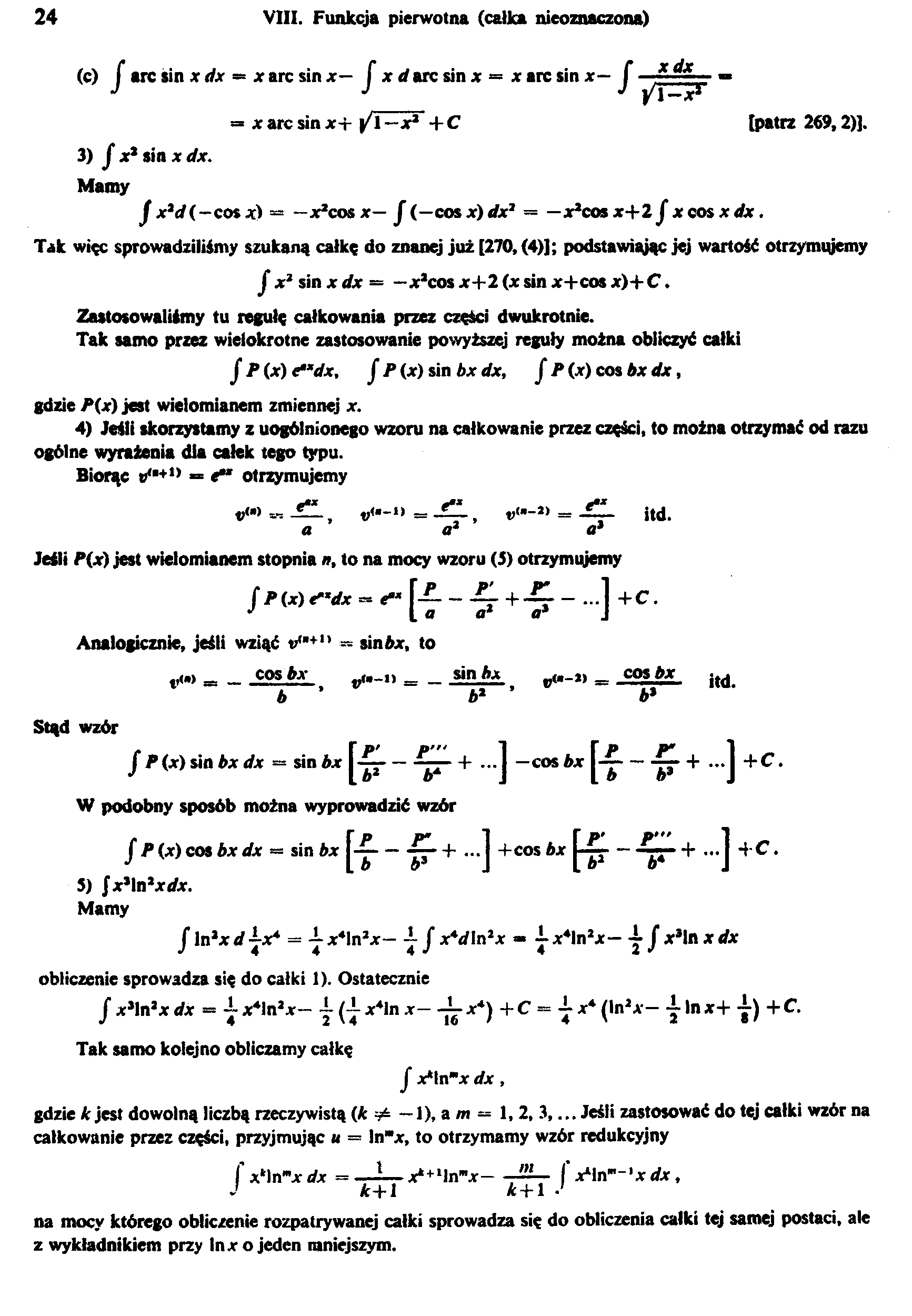
24

VIII. Funkcja pierwotna (całka nieoznaczona)

(c) f arc sin * dx — x arc sin x— fxrfarcsinx = xarcsinx- f

J    J    J y/yZr,

xdx _d \^/\-xⁱ

=■ x arc sin x+ /l-x² + C    [patrz 269,2)].

3)    f x² sin * dx.

Manty

| x²d(—cos jc> = —x²cos *— J (—cos x) rfx² = —x*cos x-f 2 J * cos x dx.

Tak więc sprowadziliśmy szukaną całkę do znanej już [270, (4)]; podstawiając jej wartość otrzymujemy

j x¹ sin x dx = — x²cos jc+2 (x sin jc+cos x)+ C.

Zastosowaliśmy tu regułę całkowania przez części dwukrotnie.

Tak samo przez wielokrotne zastosowanie powyższej reguły można obliczyć całki

J P (x) e“*dx,    J P (x) sin bx dx, J P (x) cos bx dx,

gdzie P(x) jest wielomianem zmiennej x.

4)    Jeśli skorzystamy z uogólnionego wzoru na całkowanie przez części, to można otrzymać od razu ogólne wyrażenia dla całek tego typu.

Biorąc o'^,+1> = e" otrzymujemy

***

itd.

k

a    a*    a*

Jeśli P(x) jest wielomianem stopnia u, to na mocy wzoru (J) otrzymujemy

jP(x)P^,’dx    J-r +—■ ~ -1 +C.

^J    l a a¹ a⁹ J

Analogicznie, jeśli wziąć t/"⁺ⁿ ~ sinbx, to

— —

cos bx b

pii-n ₌ _

sin hx b²

»<•-» =

cos bx b*

itd.

Stąd wzór

jP(x) sin bx dx = sinóx |p—    + ...j — cos bx    + ...j +C.

W podobny sposób można wyprowadzić wzór

fP(x)cos bxdx <= sin bx — ■— + ...J +cos bx    + ...J 4-C.

5) Jx*ln²xrfx.

Mamy

J ln²xdjx* = -i-x⁴ln²x— -i j x*dln²x - yx⁴ln²x— y J x*ln xdx

obliczenie sprowadza się do całki 1). Ostatecznie

j x²ln²xdx = -~x⁴ln²x— y (-i-x⁴lnx—jyx⁴) + C = y x⁴(ln²x— y lnx+ y) +C.

Tak samo kolejno obliczamy całkę

J x*ln"x dx,

gdzie k jest dowolną liczbą rzeczywistą (k # — 1), a m = 1, 2, 3,... Jeśli zastosować do tej całki wzór na całkowanie przez części, przyjmując u = ln“x, to otrzymamy wzór redukcyjny

f x*ln^mxdx =—-—x*⁺¹ln"x—    f x^tln^m~'xdx_f

J    *+l    A + l •'

na mocy którego obliczenie rozpatrywanej całki sprowadza się do obliczenia całki tej samej postaci, ale z wykładnikiem przy lnxo jeden mniejszym.