filtr10

Huch wód gruntowych .'Mli [R. VIII

przepuszczalnym wytnijmy prostokątny słupek o wymiarach dxdy sięgajmy od nieprzepuszczalnego podłoża do zwierciadła wody gruntowej (rys. 166). Jeżeli ruch jest trwały, to położenie zwierciadła wody pozostaje niezmienne w czasie. Przepływ przez górną i dolną ściankę wyciętego słupka równa się oczywiście zeru. Rozpatrzmy przepływy przez ścianki boczne. Przez ściankę równoległą do osi y o współrzędnej x przepływu zgodnie z prawem Dupuit

dz    k d(z²)

k z -— dy — — ^—- dy . dx    2 dx

Przez równoległą do niej ściankę odległą o dx przepływ^ wynosi

d(z²)

dx

d\z>)

dx²

dx

dy.

Różnica przepływów przez te ścianki wyniesie oczywiście

k d²(z²)

2 dx²

dx dy .

Analogicznie różnica przepływów⁷ przez ścianki równoległe do osi x równa

k d²(z²)

--—dxdy.

2 dy²

Pizy ciągłości ruchu i założeniu cieczy nieściśliwej ogólna różnica przepływów lówna się zeru, stąd zależność

(188)

dHz²) . dHz²)

—— + —— = 0 . dx²    dy²

Z lego warunku możemy wysnuć następujący wniosek.

Jeżeli równanie (188) spełniają funkcje

4 = /i(«, y),    4 = f*{x»y),    4 =fz(^x> y) *td.,

In spełni go również funkcja

z² = U(x, y) + f_t(x, y) + f₃(x, y) + ...

A Ina z przejdziemy do rozpatrzenia równoczesnego działania zespołu stu-il/icn opuszczonych do poziomej warstwy nieprzepuszczalnej.

Przy jednoczesnym działaniu zespołu studzien dostatecznie blisko siebie pnlozoiiych będą one wzajemnie na siebie oddziaływały. Rozpatrzmy, jaki będzie poziom wody w jakimś punkcie A przy równoczesnym działaniu zespołu studzien o promieniach r_v r_2; r₃,..., r_n, jeżeli wydatki każdej zo r| udzlen wynoszą odpowiednio q_v q_r    q_n (rys. 167). Oznaczmy ponadto

odległości każdej ze studzien od badanego punki u przez x_v .r_a,    x_n.

Gdyby każda ze studzien działała oddzielnie, to do obliczenia rzędnej zwierciadła w^Tody stosowalibyśmy wzory (163), mianowicie:

^r2    2rr- in Jb*

.    .    .    2r₃

Rys. 167

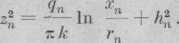
W oparciu o podaną zależność (188) możemy napisać

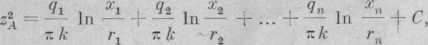
§ 54]

Jednoczesne działanie zespołu studzien

(1HU)

przez z_A rozumiemy tu wzniesienie zwierciadła wody w punkcie A ponad warstwą nieprzepuszczalną (w przypadku poziomej warstwy nieprzepus/.rzal nej).

Przyjmując często spotykany w praktyce przypadek, że promienie i wydatki wszystkich studzien są jednakowe, czyli że = r₂ = ... r_H r oraz ^ = q₂ = ... = q_n = q, otrzymamy równanie

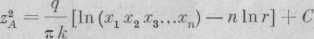
lub

— In (x₁x₂x_z.. .x_n) — lnr + C ,

w równaniu tym n q = Q oznacza łączny wydatek wszystkich studzien. Wprowadzając to oznaczenie mamy

k n

- In (x₁ x₂ x₃.. .x_n) — lnr

C.

Należy jeszcze wyznaczyć wartość stałej C. W tym celu rozpatrzmy punkt znajdujący się na granicy zasięgu działania całego zespołu studzien. Po nieważ zasięg ten jest dostatecznie duży w porównaniu z odległościami między poszczególnymi studniami, możemy przyjąć, że* odległości wszy, I kich studzien od tak obranego punktu są sobie równe, a więc