filtr8

Ruch wód gruntowych 342 LR. VIII

Rozwiązując równanie (172) względem q otrzymujemy h

? = -

g<p²UL 2 k

11-h

h \* 2k²h(H + h)

H — h

lub oznaczając h — all (gdzie 0<!a<^l) oraz K

g<p² L²II 2 k²Il

(173)

otrzymujemy

q =

2 k

1-a

V

/ / a

1 —a

+ K(i +

a) aj.

(173')

Ze wzoru tego wynika, że gdy a maleje począwszy od skrajnej wartości //    1, przepływ q rośnie aż do chwili, gdy a osiąga pewną wartość a₀. Gdy a

maleje w dalszym ciągu, czyli w przedziale a₀ > a 0, q maleje. Nie jest lo zgodne z warunkami fizycznymi. Niezgodność łatwo wytłumaczyć tym, ze z chwilą gdy a staje się mniejsze od a₀, następuje swobodny wypływ wody ze ścianki grobli i przyjęte przez nas założenie ruchu wolnozmiennego upada. Nie mamy już prawa stosować równania Bernoulliego do całości strumienia. Przeto równania (173) i (173^r) są ważne tylko dla przedziału 1 a a₀. W ton sposób wartość a₀ określa nam graniczną wartość h, poniżej której rozpoczyna się swobodny wypływ wody ze ścianki. Oczywiście prędkość wypływu przy swobodnym wypływie jeszcze nieco wzrasta.

Obliczając warunek, przy którym q osiąga maksimum, dochodzimy do zależności

K = —

8 a*

(1+2 a₀)² (1 — a₀)

G; ⁼ /(^ao) •

(174)

Rachunkowo dość trudno jest wyznaczyć wartość a₀ z podanego równania. Praktycznie wygodniej jest sporządzić tabelę lub wykres funkcji /(a₀) i z nich odczytywać a₀ dla poszczególnych wartości

K =

2 k² H

=/(«o) •

§ 51. Studnie artezyjskie

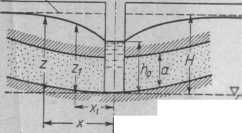
Studnia artezyjska przy warstwie wody stojącej. Jak wiemy, wodą arii' /y I ką nazywamy wodę gruntowy znajdującą się pod 'ciśnieniem międ/\ dwiema warstwami nieprzepuszczalnymi. Studnię sięgającą do warstw) wody artezyjskiej nazywamy artezyjską. Ponieważ woda znajduje się pod ciśnieniem, przoto w^r studni woda podniesie się w⁷ porównaniu z górną wni siwą nieprzepuszczalną, musi bowiem dojść do poziomu piezoinetrycznej linii ciśnień. Rozpatrzmy studnię sięgającą dnem do dolnej warstwy nie przepuszczalnej, przy tym przyjmujemy, że warstwa wodonośna ma stałą grubość a (rys. 164).

Oczywiście mając do czynienia z wodą pod ciśnieniem będziemy opero wali nie spadkiem zwierciadła wody, lecz spadkiem linii ciśnień. II oznacza tu, jak widać z rysunku, wzniesienie linii ciśnień przed rozpoczęciem pom powania (przy założeniu, że mamy warstwę stojącej wody artezyjskiej).

poziom, porównawczy

Rozumowanie prowadzimy podobnie jak przy swobodnym zwierciadle wody grun- pierwotny poziom linii ciśnień -towej.

A więc    •    dz

Q = 2nxak-,

^V    dx

dz =

Q dx

Rys. 164

X In-,	(175
X
ln r	(176;

2xak x

po scałkowaniu

z z, ⁼

przy z_x = h₀, x_x = r

z h_n

2 TC a k

Podstawiając z = H, x = H otrzymamy

(177)

2 r._ak

<? = — (^H~^h•)•

In—’ r

Studnia artezyjska przy warstwie wody płynącej. Znów przyjmujemy, że grubość warstwy wodonośnej jest stała i równa się a. Przy wodzie pły nącej linia ciśnień przed rozpoczęciem pompowania nie będzie poziomu, lecz ułoży się z jakimś spadkiem równym i. (Zwróćmy uwagę, że warst wa wodonośna może nie być równoległa do linii ciśnień).

Po to, żeby przeprowadzić rozumowanie analogicznie jak przy studniach opuszczonych do strumienia o sw^robodnym zwierciadle i pochyłej warstwie nieprzepuszczalnej, przez H będziemy rozumieli stałą wartość równą wznic sieniu linii ciśnień (przed powstaniem depresji) ponad dnom studni (przy strumieniu o swobodnym zwierciadle była to stała głębokość strumienia). W wyniku otrzymamy następujące wzory:

Równanie powierzchni ciśnień

Q l/x^l 4- ?/²

z — xi^ H+—~ ln^L--¹ .    (178)

2 nka It