Str 104

duje się poniżej otworu (rys. 7.1), to otwór nazywamy niezatopionym, a wypływ z niego — swobodnym. Jeśli natomiast zwierciadło znajduje się powyże otworu, wypływ jest zatopiony (rys. 7.4). Jeżeli ciecz przykrywa otwór częściowo, to otwór taki nazywamy częściowo zatopionym; do obliczeń dzielim\ go na dwie części: zatopioną i nie zatopioną i każdą z nich obliczamy oddzielnie. Wydatek takiego otworu jest równy sumie wydatków z obu części otworu.

Drugi podział wynika z analizy rozkładu prędkości w otworze; szczególnie chodzi o prędkość w najwyższym i najniższym punkcie otworu. Jeżeli różnica między tymi prędkościami jest mała w stosunku do prędkości średniej -otwór nazywamy małym, jeżeli różnica ta ma istotne znaczenie — otwór traktujemy jako duży. W przypadku otworów nic zatopionych prędkość w każdym punkcie otworu zależy od jego zagłębienia. Względne różnice prędkości zależą więc od stosunku wysokości otworu do jego zagłębienia.

W obliczeniach praktycznych otwór można traktować jako mały, jeżeli jegc wysokość (różnica zagłębień najniższego i najwyższego punktu otworu) nie przekracza 25% zagłębienia środka ciężkości otworu. Kryterium podziału na otwory małe i duże traci sens w odniesieniu do otworów zatopionych, ponieważ w tym przypadku zagłębienie poszczególnych części otworu nic ma wpływu na panujące w nich prędkości, zależą one bowiem wyłącznie od różnicy poziomów cieczy po obu stronach otworu.

Wypływ z małego otworu niezatopionego

Rozpatrzmy wypływ z otworu pokazanego na rys. 7.1. Zgodnie z określeniem otworu małego możemy przyjąć, że prędkości w całym jego przekroju są jednakowe i równe u, a ciśnienie p.

Ułóżmy równanie Bernoulliego dla przekroju pionowego ustawionego w pewnej odległości przed otworem i przekroju strumienia, tzn. za otworem. W przekroju pierwszym prędkość średnia jest równa u„, a ciśnienie na powierzchni w zbiorniku wynosi p_Q.

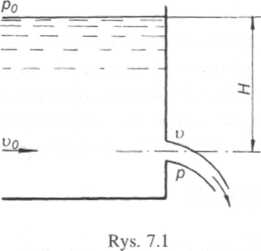
Jako poziom porównawczy przyjmijmy poziom przechodzący przez środek otworu. Wtedy

P₀ ⁺ V^H    uo

—-+ a —

Y    2g

= £₊JL

2g

str*

Mamy tu do czynienia z jedną stratą lokalną przy wlocie do otworu

h

str

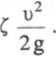
104