wymaganiar bmp

3. Roztwory rzeczywiste

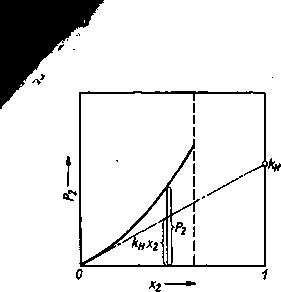
Rys. 3.24. Wyznaczenie współczynnika aktywności f₂ z pomiarów prężności cząstkowej pary składnika 2 nad roztworem: fi = P/knTi

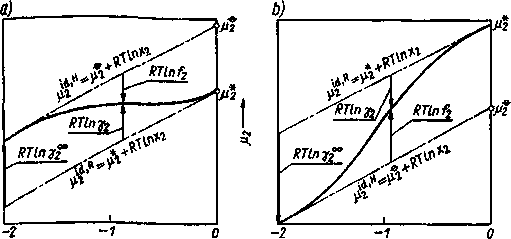
Zależność pomiędzy współczynnikami aktywności w symetrycznym i niesymetrycznym układzie odniesienia przedstawiono na rys. 3.25 otrzymanym w wyniku nałożenia na siebie rys. 3.23 oraz 3.4. Proste fi^'^R oraz opisane odpowiednio wyrażeniami (2.35) oraz (3.11) reprezentują zależności potencjału chemicznego składnika 2 od jego ułamka molowego w roztworach doskonałych odpowiednio w sensie prawa Raoułta i prawa Henry’ego. Różnica potencjałów chemicznych p® - /ij określa graniczną wartość, do której dąży współczynnik aktywności 72, gdy ułamek molowy x₂ dąży do zera - oznacza się ją 7.J⁰.

= exp    (³-¹²⁵)    \

Rysunek 3.25 pokazuje, że niezależnie od znaku odchyleń od t prawa Raoułta, współczynniki aktywności wiąże relacja

RTI117J⁰ = RTln 72 - RT ln f₂    (3.126)

którą można zapisać w postaci równoważnej

h =

(3.127)

72

-,00

72

3.8. Niesymetryczny układ odniesienia

111

lnX2-in X2-»-

Rys. 3.25. Interpretacja geometryczna współczynników aktywności w dwu układach odniesienia: a) dodatnie odchylenia od prawa Raoułta, b) odchylenia ujemne

Przykład 3.11. Porównanie współczynników aktywności w dwu układach odniesienia.

Na podstawie izotermicznych danych równowagowych układu ciecz-para obliczyć wartości współczynników aktywności w symetrycznym i niesymetrycznym układzie odniesienia składników roztworu: cykloheksan (1) - anilina (2).

Dane: Równowagowe dane¹ badanego układu w temp. t — 50,2°C zestawiono w trzech pierwszych kolumnach tabl. 3.6. Podano sumaryczna prężność pary nasyconej P oraz skład fazy ciekłej x-> i gazowej j/2- Prężności par nasyconych czystych składników wynoszą odpowiednio: P* = 273, 0 Tr oraz Pj = 3,47 Tr.

Rozwiązanie: Z uwagi na dużą dysproporcję prężności par nasyconych czystych składników faza gazowa zawiera znaczną przewagę składnika bardziej lotnego więc wyznaczenie składu pary jest trudne doświadczalnie. Współczynniki aktywności w symetrycznym układzie odniesienia (72 i 71) autorzy cytowanej pracy obliczyli ze wzorów (3.30) z pominięciem niedoskonałości fazy gazowej - błąd wynikający z tego uproszczenia jest pomijalny w porównaniu z dokładnością pomiaru. Wyniki obliczeń zestawiono w czwartej i piątej

1

L.Abello i in.: Buli.Soc.Chim.France. 1968, 11,4360.