instalacje115

4. TEORIA SILNIKÓW SKOKOWYCH 112

Moc maksymalna występuje kiedy /? = 0, punktem pracy zaś jest E. W warunkach obciążenia maksymalną mocą kąt obciążenia & jest równy ę.

Równanie maksymalnej możliwej mocy (kiedy punktem pracy jest E) może być ułożone na podstawie równań (4.43) i (4.46) przy /? — 0 z podstawieniem modułu z równania (4.42)

_ o>N<P_mU _ <o*N*<HR

^r'““ _v !«- -,«/ )=]    [K- + (a>vĄ    ¹ ' '

Odpowiednie wyrażenie na moment elektromagnetyczny wytwarzany przez dwupasmowy, dwubiegunowy silnik

(4.49)

M_e —2

Podstawienie (4.48) do (4.49) daje wzór na moment obrotowy wyrażony za pomocą parametrów silnika.

Optymalne warunki uzyskiwania mocy maksymalnej można określić za pomocą dwu parametrów. Pierwszym z nich jest bezwymiarowy parametr k_p, określany jako

k_p =

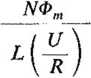
(4.50)

który jest miarą względnej „siły” magnesu i uzwojenia.

Drugim parametrem jest stała czasowa T, określona jako

T = A    (4.51)

Warunek uzyskania mocy maksymalnej możliwej przy prędkości Q_nt może być wyrażony jednym prostym równaniem

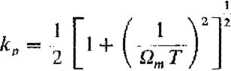
(4.52)

Silnik skokowy o danych k_p i T ma tylko jedną prędkość, przy której można uzyskać moc maksymalną. Przy prędkościach powyżej lub poniżej zdefiniowanego równaniem (4.52) optimum, silnik i napęd będą niedopasowane i otrzymana moc będzie mniejsza niż możliwa do uzyskania w warunkach optymalnych. Silnik, którego k_p jest mniejsze niż 0,5, mocy maksymalnej nigdy nie osiągnie.

W dotychczasowych rozważaniach określano punkt pracy dla jednej prędkości, przy różnych wartościach obciążenia. W dalszym ciągu wykres kołowy Blondelła będzie pomocny przy rozpatrywaniu zachowania się silnika w szerokim zakresie prędkości w warunkach maksymalnego obciążenia przy typowych wartościach k_p.

W warunkach maksymalnego obciążenia wykres kołowy Blondelła przybiera postać przedstawioną na rys. 4.10, gdzie punktami pracy są

U

R

X

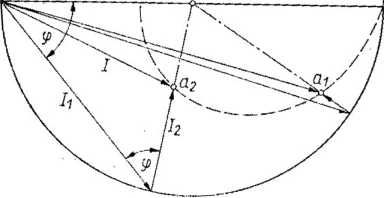
Rys. 4.10. Linia punktów pracy silnika skokowego przy zmiennej prędkości i maksymalnym obciążeniu, wyznaczona na wykresie kołowym Blondelła (wg [86])

a_x i a₂ (odpowiednio dla małych i dużych częstotliwości). Przy wzroście częstotliwości miejscem geometrycznym punktów pracy (takich jak a_v i a₂) jest krzywa, pokazana na rys. 4.10 linią przerywaną. Biorąc pod uwagę, że położenie punktu pracy na wykresie pokazuje moc mechaniczną, jest dogodnie wykreślić rodzinę krzywych roboczych, aby otrzymać wszechstronną informację o właściwościach silnika w występującym zakresie prędkości. Jest to osiągalne przez znormalizowanie prądu do podstawy UjR i wyrażenie współrzędnych punktów pracy w znormalizowanej skali. Na przykład znormalizowane współrzędne punktu pracy a₂ na rys. 4.10 wyrażają wzory

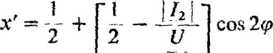
R

(4.53)

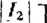
^y'~~    2 U~ ^S'^m2v

R

(4.54)

8 Silniki skokowe