s96 97

96

45.    dwoma okręgami: p = 6cosę> i p — 2\/3sm</?

7r

46.    p — tgip i prostą <p = —

47.    Obliczyć pole zawarte między krzywą y — ln(x +1) a styczną do niej w punkcie P(0,0) oraz prostą x — 2.

48.    Obliczyć pole ograniczone parabolą y = (x + 1)(2 — x) oraz stycznymi do niej poprowadzonymi w punktach przecięcia się tej paraboli z osią Ox.

49.    Obliczyć pole ograniczone parabolą y² = x, hiperbolą xy = 8 oraz odcinkiem łączącym punkt Pi (8,1) hiperboli z punktem P2(8, -\/8) paraboli.

Odpowiedzi

1. 9

3. 1

2. 6

4. i(l - ln 2)

5 2

2

7 2

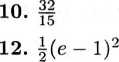
14. 1 16. 4?r

20. 2(V2- 1)

22. tc

9. 16

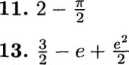
15. 3 - e

17 2 i <. ₂

19. - — l

7T

21. |

23. e + e"¹ — 2

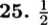
27. 7T

24.    + g(4\/3 — 9)

26. ±2

37. 4a/>arctg2 39. |jt

28. 2 30. 6tr

32. i±f-34.

5 ^v

36. 12tt 38. 7T 40. 67T

41.	7r + 3\/3	42.
43.	§7ra^2	44.
45.	|tt-3v/3	46.
47.	4 — 3 ln 3	48.
49.	^ +81n2+ f V2

2.4.2. Długości łuków

Obliczyć długości następujących łuków:

1.    y = arcsine^-*, i£[|,l),

2. x = t\ y = ^t(t²- 3), te [0,^3],

3.    p = 2asin<p, ip £ [0,7r], a > 0.

Rozwiązania

1. Gdy funkcja jest określona równaniem y = y(x), x £ [a, 6], to długość łuki tym przedziale wyraża się wzorem

L = [ \jl + [y'{x)fdx J a

przy założeniu, że funkcja ta ma ciągłą pochodną. Obliczmy pochodną

y =

1

a następnie

\/l — e^_2j:

i +    = ¹ + ! _ -pr,- [ _ _e-2. ■

Stąd

= t . ¹

Jl y/\ — e^-2x

dx.

Podstawmy

\f 1 — e~^2x = t,