skanuj0066 (34)

112

B. Cieślar

Obliczenie kątów skręcenia całkowitego ,    4MI

*******$}*

<Pc = 9a⁺9ca=--- = "Toyota J.,

Wykres kąta skręcenia całkowitego pokazano na rys. 3.7.2c.

3.8.

W stalową rurę włożono ściśle dopasowany do jej ścianek walec miedziany

(rys. 3.8.1). Całość jednym końcem sztywno zamocowano, a drugi koniec obciążono parą sił o momencie M. Obliczyć maksymalne naprężenia styczne w części stalowej, w rdzeniu miedzianym, jeżeli: M = 6 kNm, Gs = 8-10⁴ MPa, G_M = 3.85-10⁴ MPa, I = 3 m, d = 50 mm, d = 10 mm.

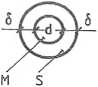
Rys. 3.8.1

Rozwiązanie

Moment obciążający M spowoduje powstanie w każdym przekroju takiego samego momentu skręcającego M₀, który zostanie przekazany na rurę stalową M_s oraz rdzeń miedziany M_m.

Z warunku statycznej równowartości otrzymamy:

M₀ = M₈ + M_m.    (1)

Ponieważ zarówno swobodny koniec rury stalowej, jak i rdzenia miedzianego obróci się o ten sam kąt, więc q>_m = <p_s,

111. Skręcanie gdzie:

113

J_m=—=61,36-10'⁸ m⁴;

32

J_{s =} rc(d-28)⁴ _ ^ _{= 174 44>}i₀-s _m4 32    32

Z równań (1) i (2) po rozwiązaniu otrzymamy:

M_m = 0,86865 kNm, M₈ = 5,13135 kNm. Maksymalne naprężenia styczne:

-    w rurze stalowej

T. ₌!E ₌ ^-³-⁵-.r ^³⁵> = 102,96 MPa;

^s J₈    174,44-10

-    w rdzeniu miedzianym

^₌om^5)_{= pa}

^m J_m    61,36-10-®

3,9.

Stalowy wał, obustronnie sztywno zamocowany, jest obciążony dwiema

parami sił (rys. 3.9.1). Zaprojektować kołowe przekroje poprzeczne pręta z warunku wytrzymałości i sztywności. W obliczeniach przyjąć: M = 300 kNm, a = 2 m, di = 1,5 d₂, G = 8-10⁴ MPa, f_d = 120 MPa, $_do_P = 0,5 °/m.

i—i-1-K-1-Łju|

Rys. 3.9.1

Rozwiązanie

Przedstawiony na rys. 3.9.2a układ jest jednokrotnie statycznie niewyznaczalny. Strona statyczna

-M_a + M - M + Md = 0.    (1)

Strona geometryczna

(2)

<p_A = 0; (Pd = 0; cp_D = (pA + <Pd,a-