str071 (5)

§ 10. RESIDUA FUNKCJI — TWIERDZENIE ROUCHEGO 71

'(r) są holomorficzne wewnątrz

unkcja zwytszająca f(z) (każde

iobliwych położonych w skon-

^C)/(:)=(TO?'

0/(z) = e^1/x.

punkt z₀ — 2 jest biegunem = z² + l oraz Q(z) = z— 2.

= 5.

ym danej funkcji. Przyjmując lamy wtedy

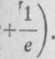
lwukrotne z_t - i, z₂ = —i,

lajpierw residuum funkcji /(z) c = 2, otrzymujemy

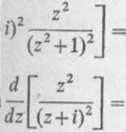
i

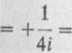
4 '

Następnie wyliczamy residuum naszej funkcji w biegunie dwukrotnym z₂ = —»• Postępując analogicznie, mamy

res_zi/(z) = lim —

z^-tdz

d

= lim — z—idz

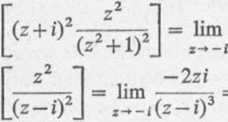
d T (z + i)²z²    "1

dzl_(z+j)² (z-0²J

+2i² _ -2 ⁼ (-2i)³ ~ ^8? “

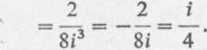
d)    /(z) = e^z+i,z. Funkcja nasza ma w punkcie z₀ = 0 punkt istotnie osobliwy. W celu obliczenia residuum w tym punkcie rozwijamy funkcję w otoczeniu pierścieniowym 0<|z|<oo na szereg Laurenta. Mamy wtedy

/(z) = e^I+1/l = eV^/x =

Wymnażając szeregi występujące w ostatniej równości i zbierając wyrazy zawierające 1/z, otrzymujemy, że współczynnik a_ _t rozwinięcia funkcji /(z) w szereg Laurenta ma postać

00

^{w o!_i}-

n-0

Zgodnie ze wzorem (10.1) wzór (♦) określa residuum naszej funkcji w punkcie z = 0.

e)    /(z) = cos-. Rozwijamy naszą funkcję na szereg Laurenta. Mamy wtedy dla

z

(ZS)(SśO-

n = 0    n = 0

0 < |z| <oo

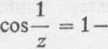
1 _1___1_

p2! ⁺ ?4!^_'?ó]

+

1

Z rozwinięcia tego wynika, że punkt z — 0 jest punktem istotnie osobliwym rozważane funkcji i że residuum tej funkcji w punkcie z₀ = 0 równa się zeru, bo a_i = 0.

f) /(z) = e^1/z. Rozwijając naszą funkcję w szereg Laurenta w otoczeniu 0<|z|<oo, mamy

/(z) = e^llz

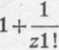
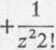
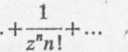
Z rozwinięcia tego wynika, że punkt z₀ = 0 jest punktem istotnie osobliwym danej funkcji i że residuum tej funkcji w punkcie z₀ = 0 równa się 1, bo = 1.

Zadanie 10.2. Znaleźć wartość całki zdz

a)    '

b)

I??

c

f e^!dz

J(z² + 1)²’

. ₂ > gdzie C jest konturem o równaniu x²+y² = 4, sm z

gdzie C jest konturem o równaniu x² + 4y²—8y = 0.