str193 (3)

(WANIA § 6. WYZNACZANIE CAŁKI OGÓLNEJ RÓWNANIA RÓŻNICZKOWEGO RZĘDU n 193

(WANIA § 6. WYZNACZANIE CAŁKI OGÓLNEJ RÓWNANIA RÓŻNICZKOWEGO RZĘDU n 193

cładu wprowadzamy warunki

ustronnie przekształcenie La-

(1).

lmy

2

przekształceniach i uporząd-

⁽¹⁰⁾ * ‘^2L' ‘ (ś³(I7F))^+4L~¹ (śoTs⁵))^{+(1+c,) L}" ‘ (nh)'

+c₂l

Stosując twierdzenie Borela o splocie (wzór 3.9) oraz tablice przekształceń Laplace’a, wyliczamy kolejno

(U)

(12)

(13)

^L~‘ {wm} “ ^Ł"' (?) *^L" (iT?) "^ł(,!) •^(si" ⁰ “

r

=    t)² sin tc/t = cost+^t² — 1,

o

^L'iś\iW) ■ ^Ł'‘(?)*^Ł"(rT?) ⁼'^(,)'^(sta,) -

r

= J (/—t) sin t rfr = t — sin t, o

^L~¹ (sirh⁵))" ^L~¹ (I) * ^L~¹ (ff?)^=<l) *^{(sin 0} “

t

= j sinrdr = 1—cost,

L(ź) otrzymujemy

1 -c₂ CiS

l+S^{2 +}1 + S²’

s_

F-

zekształcenie Laplace’a i wy-

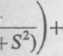
(14)

Podstawiając wzory (11), (12), (13) oraz (14) do równań (9) i (10), otrzymujemy całkę ogólną układu (1)

^    y = 3f²-r-l+(l + C₁)cosf+(2-C₂)sinf,

z = f² + 2+(C₂ —2)cosi+(l + C₁)sini.

Uwaga 1. Znajomość całki ogólnej danego równania różniczkowego (układu równań różniczkowych) pozwala rozwiązać zagadnienie brzegowe dla tego równania (układu równań).

Uwaga 2. Rozwiązanie ogólne może być wykorzystane również w tym przypadku, gdy wartości funkcji i jej pochodnych dane są tylko w jednym punkcie, czyli gdy szukamy rozwiązania przy warunkach początkowych w punkcie t₀ =£ 0.

Zadania do rozwiązania

1. Znaleźć rozwiązanie ogólne równania:

a)    y"’-3ay"+3a²y'-a³y = e^at,

b)    y'"-2y"-3y' + l0y = 0,

c)    4y⁽⁴⁾-12y’"+Uy"-3y' = 4cos/.

13 — Wybrane działy matematyki...