img460 (2)

e) funkcja ^ jest różniczkowalna w zbiorze {x e A n 8: g(x) * 0} i

(x)

f'(x) ■ g(x) ~f(x) -g'(x) l9(*)}²

(jest to wzór na funkcję pochodną ilorazu).

Często przy obliczaniu pochodnych nie podaje się dziedzin: ani funkcji /, ani pochodnej /'. Rozumiemy wtedy, że dziedzinami tymi są odpowiednio zbiory D_f i Df tych wszystkich argumentów, dla których wzory funkcji i funkcji pochodnej mają sens liczbowy (przy czym pamiętamy, że musi spełniony być warunek

Df <= D_f).

Zastosujemy teraz twierdzenie 4. do obliczania pochodnych bardziej skomplikowanych funkcji.

razY&tu 6.

Wyznaczmy pochodne następujących funkcji:

4

^a)    f{x) = 4x³ + x³ ;

b)    f(x) = (x + Vx ) • (    + 1 );

c)    f(x) =    .

X + 1

Ad a) D_f = (0, +oo). Wyznaczamy funkcję pochodną:

(

4x³ + x³

V

.V

= (4x³)' + x ³ = 4 • (x³)' +

ytw.4b ^v    \ ytw.4a

x³ = 4 • 3x² + --x³ = 12x²    %(

V ytw.3    3    3

Tak więc f'(x) = 1 2x² + ^ Vx, Df = (0, +oo).

Ad b) Wbrew pokusie, aby zastosować wzór na pochodną iloczynu, przekształcimy najpierw wzór naszej funkcji:

/(x) = (x + Vx) • (Vx2 + 1) =

f i]		2 ^
X + X^2		X^3 + 1
V >		^ J

5 z    1

= x³ + x⁶ + x + x² , D_f = (0, +oo).

leraz już łatwo znajdujemy:

f

5    7

r³ + x⁶ + x + x²

y	f s)	' (t)	t
zz	X^3	+ X^6	+ (x)' +	X^2
y tw. 4b	V J	V >		V y

= |x³+|x⁶+¹ + ^x² = |^x2 + ^⁶Vx+1 + —1_, 3    6    2    3    6    2yx

tak więc

f'(x) = |    | ⁶Vx + Aj + 1 , Df.= (O, +Q0).

Ad c) D_f = (-oo, -1 )u(-1, +<x>). Korzystając tym razem ze wzoru na pochodną ilorazu, mamy:

r ,Y

x- 1

_vx+1_y

_ (x- 1)' • (X + 1)-(x- 1) • (x + 1)'. (x+1)²

_ 1-(x + 1) - (x - 1)-1 _    2

(X+1)²    (X + 1) ²

Zatem f'(x) =

(x+1)²

, Df = (-oo, -1)u(—1, +co).

PIHIfll I.

W odległości x przed wypukłą soczewką o ogniskowej 5 cm ustawiono przedmiot P (x > 5). Oznaczmy przez y odległość obrazu Q tego przedmiotu od soczewki. Znajdziemy wzór funkcji określającej szybkość zmiany y w zależności od x. Jaka będzie szybkość zmiany y, jeśli przedmiot ustawimy w odległości 55 cm, a następnie będziemy zmieniać jego położenie?

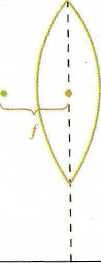
P.

X