instalacje145

6. BADANIA SILNIKÓW SKOKOWYCH 170

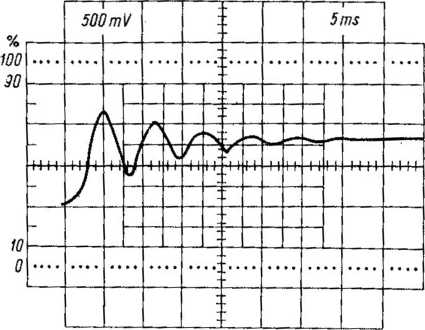
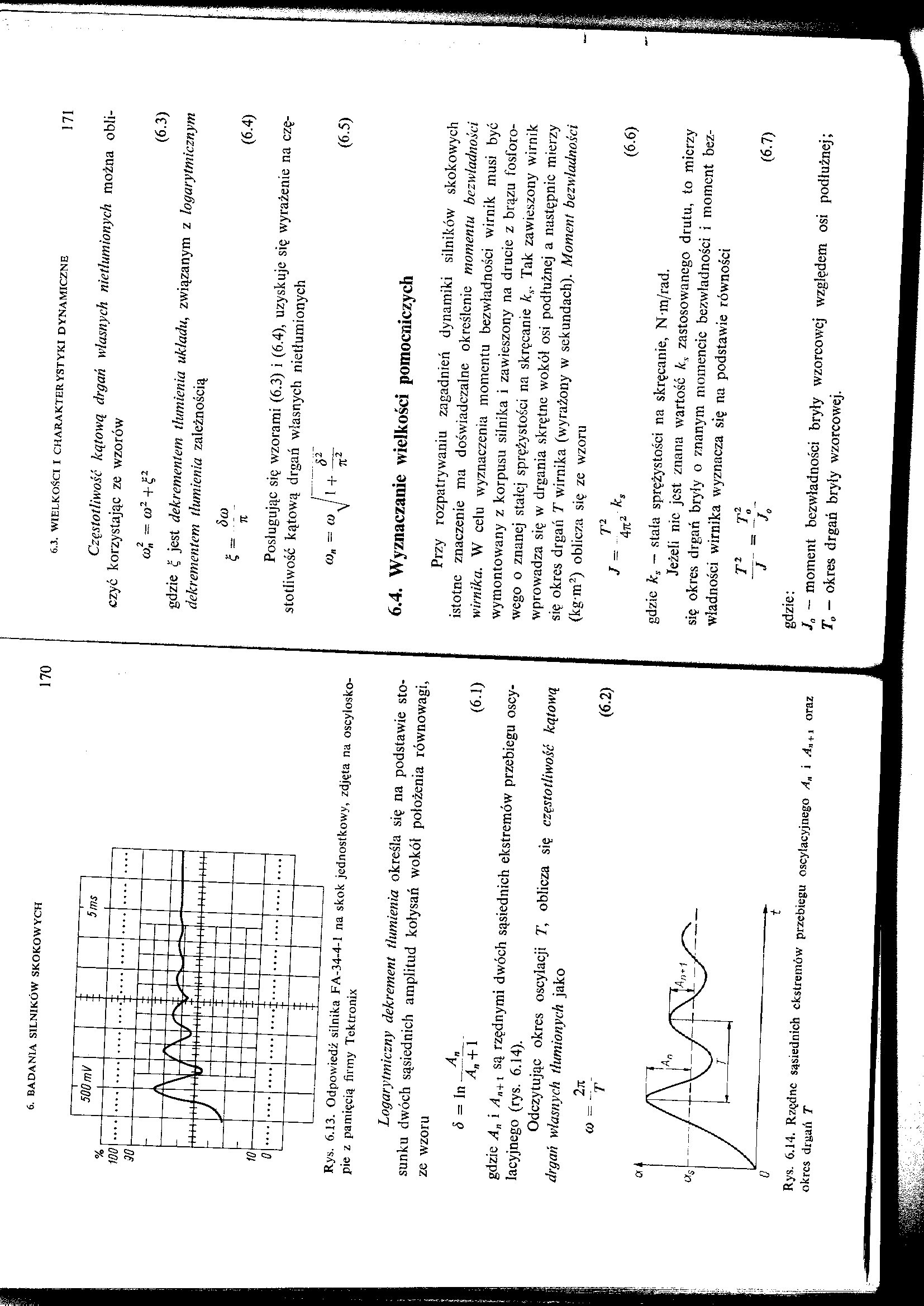
Rys. 6.13. Odpowiedź silnika FA-34-4-1 na skok jednostkowy, zdjęta na oscyloskopie z pamięcią firmy Tektronix

Logarytmiczny dekrement tłumienia określa się na podstawie stosunku dwóch sąsiednich amplitud kołysań wokół położenia równowagi, ze wzoru

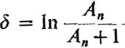
(6.1)

gdzie A„ i A_n+t są rzędnymi dwóch sąsiednich ekstremów przebiegu oscylacyjnego (rys. 6.14).

Odczytując okres oscylacji T, oblicza się częstotliwość kątową drgań własnych tłumionych jako

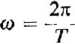
(6.2)

Rys. 6.14. Rzędne sąsiednich ekstremów przebiegu oscylacyjnego A_n i A_{n + l} okres drgań T

oraz

Częstotliwość kątową drgań własnych nietłumionych można obliczyć korzystając ze wzorów

(6.3)

gdzie £ jest dekrementem tłumienia układu, związanym z logarytmicznym dekrementem tłumienia zależnością

Posługując się wzorami (6.3) i (6.4), uzyskuje się wyrażenie na częstotliwość kątową drgań własnych nietłumionych

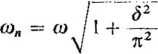
(6.5)

6.4. Wyznaczanie wielkości pomocniczych

Przy rozpatrywaniu zagadnień dynamiki silników skokowych istotne znaczenie ma doświadczalne określenie momentu bezwładności wirnika. W celu wyznaczenia momentu bezwładności wirnik musi być wymontowany z korpusu silnika i zawieszony na drucie z brązu fosforowego o znanej stałej sprężystości na skręcanie k_s. Tak zawieszony wirnik wprowadza się w drgania skrętne wokół osi podłużnej a następnie mierzy się okres drgań T wirnika (wyrażony w sekundach). Moment bezwładności (kg m²) oblicza się ze wzoru

gdzie k_x — stała sprężystości na skręcanie, N-m/rad.

Jeżeli nic jest znana wartość k._x zastosowanego drutu, to mierzy się okres drgań bryły o znanym momencie bezwładności i moment bezwładności wirnika wyznacza się na podstawie równości

(6.7)

T² _ Tl

J J₀

gdzie:

— moment bezwładności bryły wzorcowej względem osi podłużnej; T₀ — okres drgań bryły wzorcowej.